
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动. 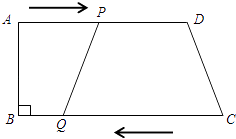
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.
【答案】
(1)解:设经过x(s),四边形PQCD为平行四边形
即PD=CQ
所以24﹣x=3x,
解得:x=6
(2)解:设经过y(s),四边形PQBA为矩形,
即AP=BQ,
所以y=26﹣3y,
解得:y= ![]()
(3)解:设经过t(s),四边形PQCD是等腰梯形.
过Q点作QE⊥AD,过D点作DF⊥BC,
∴∠QEP=∠DFC=90°
∵四边形PQCD是等腰梯形,
∴PQ=DC.
又∵AD∥BC,∠B=90°,
∴AB=QE=DF.
在Rt△EQP和Rt△FDC中,
![]() ,
,
∴Rt△EQP≌Rt△FDC(HL).
∴FC=EP=BC﹣AD=26﹣24=2.
又∵AE=BQ=26﹣3t,
∴EP=AP﹣AE=t﹣(26﹣3t)=2.
得:t=7.
∴经过7s,PQ=CD
【解析】(1)设经过ts时,四边形PQCD是平行四边形,根据DP=CQ,代入后求出即可;(2)设经过ts时,四边形PQBA是矩形,根据AP=BQ,代入后求出即可;(3)设经过t(s),四边形PQCD是等腰梯形,利用EP=2列出有关t的方程求解即可.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


科目:初中数学 来源: 题型:
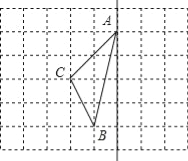
【题目】如图,在8×6正方形方格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线![]() 成轴对称的△AB′C′,并回答问题:
成轴对称的△AB′C′,并回答问题:
图中线段CC′被直线l ;
(2)在直线l上找一点D,使线段DB+DC最短.(不写作法,应保留作图痕迹)
(3) 在直线l确定一点P,使得|PA-PB|的值最小.(不写作法,应保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2 . 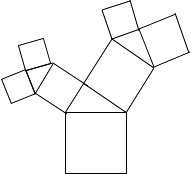
A.28
B.49
C.98
D.147
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com