
【题目】先化简,后求值:a(a+1)﹣(a+1)(a﹣1),其中a=3.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根.比如对于方程![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程的系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C的横坐标m即为该方程的一个实数根(如图1);
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D的横坐标n即为该方程的另一个实数根.
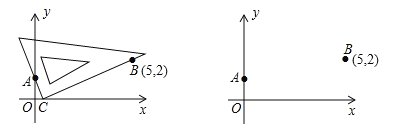
(1)在图2中,按照“第四步”的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹);
(2)结合图1,请证明“第三步”操作得到的m就是方程![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程![]() (a≠0,
(a≠0,![]() ≥0)的实数根,请你直接写出一对固定点的坐标;
≥0)的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当m1,n1,m2,n2与a,b,c之间满足怎样的关系时,点P(m1,n1),Q(m2,n2)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是30cm和19cm,则△ABC的腰和底边长分别为( )
A.11cm和8cm
B.8cm和11cm
C.10cm和8cm
D.12cm和6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
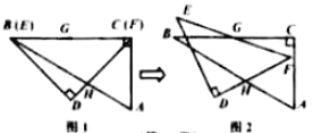
【题目】一副含![]() 和
和![]() 的三角板
的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,现将三角板
,现将三角板![]() 绕点
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,观察点
的变化过程中,观察点![]() 的位置变化,点
的位置变化,点![]() 相应移动的路径长为 (结果保留根号).
相应移动的路径长为 (结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
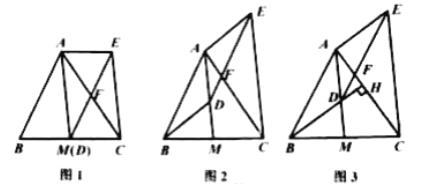
【题目】如图![]() 是
是![]() 的中线,
的中线,![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合),
重合),![]() 交
交![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
(1)如图1,当点![]() 与
与![]() 重合时,求证:四边形
重合时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 不与
不与![]() 重合时,(1)中的结论还成立吗?请说明理由.
重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() .当
.当![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA.若﹣3am﹣1b2与anb2n﹣2是同类项且OA=m,OB=n,求出m和n的值以及点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com