
 如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$.
如图,在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,直线EF与直线BC交于点M,若AB=2$\sqrt{2}$,BD=1,则CM的长为$\frac{1}{2}$或$\frac{3}{2}$. 分析 分析条件得出△ABD≌△ACF,从而得出CF=BD=1,FC垂直BC,由AD∥EF得知∠FMC=∠ADP,利用同角的正切值相等即可得出结论.
解答 解:根据题意可知,分两种情况:
①D点在线段BC上,连接CF,过点A做AP垂直于BC,垂足为点P,如图1,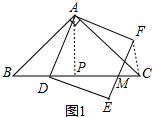
∵在△ABC中,AB=AC,∠BAC=90°,AB=2$\sqrt{2}$,
∴∠ABC=∠ACB=45°,
AP=AB×sin∠ABC=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,BP=AB×cos∠ABC=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,
又∵BD=1,BP=BD+DP,
∴DP=1,
∵∠BAC=∠DAF=90°,∠BAD+∠DAC=∠BAC,∠DAC+∠CAF=∠DAF,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF(正方形的边相等)}\end{array}\right.$,
∴△ABD≌△ACF,
∴CF=BD=1,∠ACF=∠ABD=45°,
∴∠MCF=∠ACB+∠ACF=45°+45°=90°,
在直角△APD中,AP=2,DP=1,
∴tan∠ADP=$\frac{AP}{DP}$=2,
∵EF∥AD(正方形对比平行),
∴∠FMC=∠ADP,
∴tan∠FMC=$\frac{FC}{MC}$=2,
∴MC=$\frac{1}{2}$.
②D点在线段CB延长线上,连接CF,过点A做AP垂直于BC,垂足为点P,如图2,
∵在△ABC中,AB=AC,∠BAC=90°,AB=2$\sqrt{2}$,
∴∠ABC=∠ACB=45°,
AP=AB×sin∠ABC=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,BP=AB×cos∠ABC=2$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2,
又∵BD=1,DP=DB+BP,
∴DP=3,
∵∠BAC=∠DAF=90°,∠BAD+∠DAC=∠BAC,∠DAC+∠CAF=∠DAF,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF(正方形的边相等)}\end{array}\right.$,
∴△ABD≌△ACF,
∴∠AFC=∠ADB,∠ACF=∠ABD,CF=BD=1,
∵∠ABC=45°,∠ABD+∠ABC=180°,
∴∠AFC=∠ADB=135°,
∵∠ACB=45°,
∴∠MCF=∠PCF=90°,
在直角△APD中,AP=2,DP=3,
∴tan∠ADP=$\frac{AP}{DP}$=$\frac{2}{3}$,
∵EF∥AD(正方形对比平行),
∴∠FMC=∠ADP,
∴tan∠FMC=$\frac{FC}{MC}$=$\frac{2}{3}$,
∴MC=$\frac{3}{2}$.
综合①②得知CM的长为$\frac{1}{2}$或$\frac{3}{2}$.
故答案为:$\frac{1}{2}$或$\frac{3}{2}$.
点评 本题考查了全等三角形的判定与性质,解题的关键是考虑到D点的两种情况,然后利用三角形全等得出相等的边角关系.


科目:初中数学 来源: 题型:解答题
 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.
如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,分别交AB,AC于点E,D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某城市十字路口旁有一居民区A,现在城市规划局想建设两个公交车站以方便小区居民的工作与生活,那么两车站应建在什么位置最合适呢?请你在图中画出来.
如图所示,某城市十字路口旁有一居民区A,现在城市规划局想建设两个公交车站以方便小区居民的工作与生活,那么两车站应建在什么位置最合适呢?请你在图中画出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
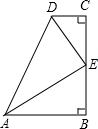 如图,已知在四边形ABCD中,AB⊥CB于B,DC⊥BC于C,DE平分∠ADC,且E为BC的中点.
如图,已知在四边形ABCD中,AB⊥CB于B,DC⊥BC于C,DE平分∠ADC,且E为BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
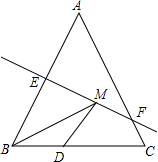 如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的动点,M为线段EF上一动点,则BM+DM最小值为6cm.
如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的动点,M为线段EF上一动点,则BM+DM最小值为6cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com