
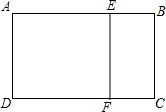
 如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$.
如图,矩形ABCD中,AB=6,BC=4,点E在AB上,EF⊥DC于点F,在边AD,DF,EF,AE上分别存在点M,N,P,Q,这四点构成的四边形与矩形BCFE全等,则DM的长度为$\sqrt{7}$. 分析 设DM=x,DN=y,则AM=4-x,根据题意得出四边形MNPQ≌矩形BCFE,得出△AMQ≌△FPN,PN=FC,MN=BC=4,∠MNO=∠PFN=∠D=90°,得出AM=FP=4-x,证明△DMN∽△FNP,得出对应边成比例$\frac{DM}{FN}=\frac{DN}{PF}=\frac{MN}{PN}$,得出FN=$\frac{x(4-x)}{y}$,PN=$\frac{4(4-x)}{y}$,根据题意得出方程组,解方程组即可.
解答 解:如图所示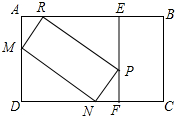
设DM=x,DN=y,则AM=4-x,
根据题意得:四边形MNPQ≌矩形BCFE,
∴△AMQ≌△FPN,PN=FC,MN=BC=4,∠MNO=∠PFN=∠D=90°,
∴AM=FP=4-x,∠DMN=∠PNF,
∴△DMN∽△FNP,
∴$\frac{DM}{FN}=\frac{DN}{PF}=\frac{MN}{PN}$,
即$\frac{x}{FN}=\frac{y}{4-x}=\frac{4}{PN}$,
∴FN=$\frac{x(4-x)}{y}$,PN=$\frac{4(4-x)}{y}$,
根据题意得:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=16}\\{y+\frac{x(4-x)}{y}+\frac{4(4-x)}{y}=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\sqrt{7}}\\{y=3}\end{array}\right.$,或$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$(舍去),
∴DM=$\sqrt{7}$;
故答案为:$\sqrt{7}$.
点评 本题考查了矩形的性质、相似三角形的判定与性质、全等三角形的判定与性质、方程组的解法等知识;本题综合性强,有一定难度,证明三角形相似,根据题意得出方程组是解决问题的关键.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:填空题
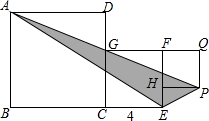 已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.
已知正方形ABCD,正方形CEFG,正方形PQFH如图放置,且正方形CEFG的边长为4,A、G、P三点在同一条直线上,连接AE、EP,那么△AEP的面积是16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com