
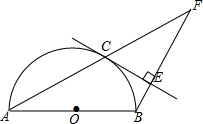
 如图,已知AB是半圆直径,EC切半圆于点C,BE⊥CE交AC的延长线于点F.求证:AB=BF.
如图,已知AB是半圆直径,EC切半圆于点C,BE⊥CE交AC的延长线于点F.求证:AB=BF. 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 “十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成.为了种植“花海”,需要从甲乙两地向大圩A、B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A、B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).
“十一”期间,包河区牛角大圩60亩的秋季花海是游客观赏的首选景点,有着独具一格的农业风情,花海由矮牵牛、孔雀菊、蓝花鼠尾草、一串红等组成.为了种植“花海”,需要从甲乙两地向大圩A、B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A、B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需人民币).| 运费(元/吨) | ||
| A | B | |
| 甲地 | 12 | 12 |
| 乙地 | 10 | 8 |
| 运往A、B两地的吨数 | ||
| A | B | |
| 甲地 | x | 50-x |
| 乙地 | ||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com