
 ),CD为△ABC的中线,⊙M与△ACD的外接圆,BC交⊙M于点N.
),CD为△ABC的中线,⊙M与△ACD的外接圆,BC交⊙M于点N.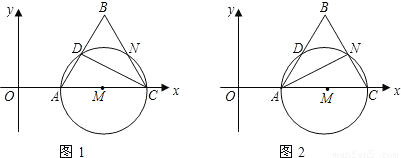
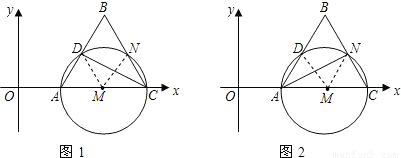 解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,
解:(1)连接MD,则∠MDA=60度,当AB绕点D,顺时针旋转使得到的直线l与圆M相切时,DM⊥AB,∠MDA=90度,所以,此时的旋转角是顺时针30度.未旋转时,点D坐标(1.5,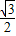 ),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=
),可设直线与x的交点为P,那么PA=AD=1,则P(0,0),设出正比例函数解析式为y=kx,过点D,所以l的解析式为:y=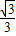 x;
x; ,
,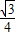 );
); ,
, );
);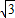 ,
,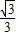 x),则PA2+PN2=AN2=3,
x),则PA2+PN2=AN2=3, ,
,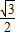 ),
),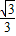 x)2+(x-
x)2+(x- )2+(
)2+(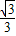 x-
x-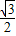 )2=3,
)2=3,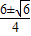 ,这是P点的横坐标,
,这是P点的横坐标,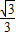 x.
x.

 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;查看答案和解析>>
科目:初中数学 来源: 题型:
 在平面直角坐标系中,将一块腰长为2
在平面直角坐标系中,将一块腰长为2| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:059
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图)

(1)按照这种规定填写下表:
(2)根据表中的数据,将s作为纵坐标,n作为横坐标,在如图所示的平面直角坐标系中找出相应各点.

(3)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数图象上,求出该函数的解析式,并利用你探求的结果,求出当n=10时,s的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京海淀区九年级第一学期期中测评数学试卷(解析版) 题型:解答题
阅读下面的材料:
小明在研究中心对称问题时发现:
如图1,当点 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 旋转180°得到
旋转180°得到 点,这时点
点,这时点 与点
与点 重合.
重合.
如图2,当点 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.



(1)请在图2中画出点 、
、 ,
小明在证明P、
,
小明在证明P、 两点关于点
两点关于点 中心对称时,除了说明P、
中心对称时,除了说明P、 、
、 三点共线之外,还需证明;
三点共线之外,还需证明;
(2)如图3,在平面直角坐标系xOy中,当 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 绕着点
绕着点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐标为(),点
的坐标为(),点 的坐为.
的坐为.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com