
分析 (1)根据“A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加l万元;B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元”即可算出承包期限为2年时A、B企业分别上缴利润的总金额;
(2)根据“A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加l万元;B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元”结合年限n以及$S=\frac{{n({{a_1}+{a_n}})}}{2}$(其中n表示数的个数,a1表示第一个数,an表示最后一个数),即可求出当年限为n年时A、B企业分别上缴利润的总金额;
(3)将n=20代入(2)的结论中,算出结果比较做差后即可得出结论.
解答 解:(1)如果承包期限2年,则A企业上缴利润的总金额为:1.5+(1.5+1)=4(万元),
如果承包期限2年,则B企业上缴利润的总金额为:0.3+(0.3+0.3)+(0.3+0.3+0.3)+(0.3+0.3+0.3+0.3)=3(万元).
故答案为:4;3.
(2)如果承包期限为n年,则A企业上缴利润的总金额为:1.5+2.5+3.5+…+(n+0.5)=(1+2+3+…+n)+0.5n=$\frac{n(1+n)}{2}$+$\frac{n}{2}$=$\frac{n(2+n)}{2}$(万元),
如果承包期限为n年,则B企业上缴利润的总金额为:0.3+2×0.3+3×0.3+4×0.3+…+(2n-1)×0.3+2n×0.3=0.3n•(1+2n)=0.6n2+0.3n.
(3)承包期限n=20时,A企业上缴利润的总金额为:$\frac{20×(2+20)}{2}$=220(万元),
承包期限n=20时,A企业上缴利润的总金额为:0.6×202+0.3×20=246(万元),
246>220,246-220=26(万元).
答:承包期限n=20时,B企业上缴利润的总金额比较多,多26万元.
点评 本题考查了列代数式以及规律型中的数字的变化类,解题的关键是:(1)根据数量关系列出算式;(2)根据规律找出通式;(3)将n=20代入(2)结论中.本题属于中档题,难度不大,解决该题型题目时,根据数字的变化规律写出通式是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>-b>-a>b | B. | -b>a>b>-a | C. | a>b>-a>-b | D. | a>-b>b>-a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
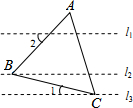 如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.
如图,直线l1∥l2∥l3,等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=35°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com