Question

13．如图，已知△ABC中，∠ABC=∠ACB，以点B为圆心，BC长为半径的弧分别交AC，AB于点D，E，连接BD，ED．
（1）写出图中所有的等腰三角形；
（2）若∠AED=114°，求∠ABD和∠ACB的度数．

Answer 1

分析 （1）根据等腰三角形的判定，两底角相等或两条边相等的三角形是等腰三角形，即可找出图中所有的等腰三角形；
（2）根据邻补角的性质可求得∠BED=66°，在△BED中可求得∠ABD=180°-2∠BED=48°，设∠ACB=x°，则∠ABC=∠ACB=x°，求得∠A=180°-2x°，又根据三角形外角的性质得出∠BDC=∠A+∠ABD，则x=180-2x+48，求得∠ACB=76°．

解答 解：（1）∵∠ABC=∠ACB，
∴AB=AC，
∴△ABC是等腰三角形；
∵BE=BD=BC，
∴△BCD，△BED是等腰三角形；
∴图中所有的等腰三角形有：△ABC，△BCD，△BED；
（2）解：∵∠AED=114°，
∴∠BED=180°-∠AED=66°．
∵BD=BE，
∴∠BDE=∠BED=66°．
∴∠ABD=180°-66°×2=48°．
解法一：设∠ACB=x°，
∴∠ABC=∠ACB=x°．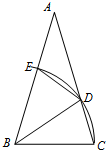
∴∠A=180°-2x°．
∵BC=BD，
∴∠BDC=∠ACB=x°．
又∵∠BDC为△ABD的外角，
∴∠BDC=∠A+∠ABD．
∴x=180-2x+48，解得：x=76．
∴∠ACB=76°．（10分）
解法二：设∠ACB=x°，
∴∠ABC=∠ACB=x°．
∴∠DBC=x°-48°．
∵BC=BD，
∴∠BDC=∠ACB=x°．
又∵∠DBC+∠BCD+∠BDC=180°，
∴x-48+x+x=180，解得：x=76．
∴∠ACB=76°．

点评 此题考查了等腰三角形的判定与性质，三角形内角和定理，三角形外角的性质，难度一般．