
【题目】某校的大学生自愿者参与服务工作,计划组织全校自愿者统一乘车去某地.若单独调配![]() 座客车若干辆,则空出
座客车若干辆,则空出![]() 个座位,若只调配
个座位,若只调配![]() 座客车若干辆,则用车数量将增加
座客车若干辆,则用车数量将增加![]() 辆,并有
辆,并有![]() 人没有座位.
人没有座位.
(1)计划调配![]() 座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
(2)若同时调配![]() 座和
座和![]() 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
【答案】(1)计划调配36座客车6辆,该大学共有210名自愿者;(2)需调配36座新能源客车4辆,22座新能源客车3辆
【解析】
(1)设计划调配36座客车x辆,该大学共有y名志愿者,则需调配22座客车(x+3)辆,根据①志愿者人数=36×调配36座客车的数量-6,②志愿者人数=22×调配22座客车的数量+12,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设需调配36座客车m辆,22座客车n辆,根据志愿者人数=36×调配36座客车的数量+22×调配22座客车的数量,即可得出关于m,n的二元一次方程,结合m,n均为正整数即可求出结论.
解:(1)设计划调配36座新能源客车![]() 辆,该大学共有
辆,该大学共有![]() 名自愿者,则根据题意得
名自愿者,则根据题意得
![]() ,解得:
,解得:![]() .
.
答:计划调配36座新能源客车6辆,该大学共有210名自愿者。
(2)设需调配36座新能源客车![]() 辆,22座新能源客车
辆,22座新能源客车![]() 辆,根据题意得
辆,根据题意得
![]() ,∴
,∴![]() .
.
又∵![]() 为正整数,∴
为正整数,∴![]() .
.
答:需调配36座新能源客车4辆,22座新能源客车3辆。


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】为了迎接全市体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的![]() 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到
名男生中随机抽取了部分男生的测试成绩(单位:米,精确到![]() 米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为
米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为![]() ,其中
,其中![]() 的频数为
的频数为![]() ,请根据有关信息解答下列问题:
,请根据有关信息解答下列问题:
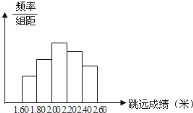
![]() 填空:这次调查的样本容量为________,
填空:这次调查的样本容量为________,![]() 这一小组的频率为________;
这一小组的频率为________;
![]() 请指出样本成绩的中位数落在哪一小组内,并说明理由;
请指出样本成绩的中位数落在哪一小组内,并说明理由;
![]() 样本中男生立定跳远的人均成绩不低于多少米;
样本中男生立定跳远的人均成绩不低于多少米;
![]() 请估计该校初三男生立定跳远成绩在
请估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有多少人?
米)的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
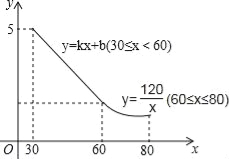
【题目】某工艺品厂生产一种汽车装饰品,每件生产成本为20元,销售价格在30元至80元之间(含30元和80元),销售过程中的管理、仓储、运输等各种费用(不含生产成本)总计50万元,其销售量y(万个)与销售价格(元/个)的函数关系如图所示.
(1)当30≤x≤60时,求y与x的函数关系式;
(2)求出该厂生产销售这种产品的纯利润w(万元)与销售价格x(元/个)的函数关系式;
(3)销售价格应定为多少元时,获得利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:2019年11月2日-4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
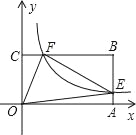
【题目】如图,平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴的正半轴上,反比例函数y=![]() 在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F,已知BE=2AE,四边形的OEBF的面积等于12.
在第一象限的图象分别交矩形OABC的边AB、BC边点于E、F,已知BE=2AE,四边形的OEBF的面积等于12.
(1)求k的值;
(2)若射线OE对应的函数关系式是y=![]() ,求线段EF的长;
,求线段EF的长;
(3)在(2)的条件下,连结AC,试证明:EF∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读如下材料,然后解答后面的问题:已知直线l1:y=﹣2x﹣2和直线l2:y=﹣2x+4如图所示,可以看到直线l1∥l2,且直线l2可以由直线l1向上平移6个长度单位得到,直线l2可以由直线l1向右平移3个长度单位得到.这样,求直线l2的函数表达式,可以由直线l1的函数表达式直接得到.即:如果将直线l1向上平移6的长度单位后得到l2,得l2的函数表达式为:y=﹣2x﹣2+6,即y=﹣2x+4;如果将直线l1向右平移3的长度单位后得到得l2,l2的函数表达式为:y=﹣2(x﹣3)﹣2,即y=﹣2x+4.
(1)将直线y=2x﹣3向上平移2个长度单位后所得的直线的函数表达式是 ;
(2)将直线y=3x+1向右平移m(m>0)两个长度单位后所得的直线的函数表达式是 ;
(3)已知将直线y=![]() x+1向左平移n(n>0)个长度单位后得到直线y=
x+1向左平移n(n>0)个长度单位后得到直线y=![]() x+5,则n= .
x+5,则n= .
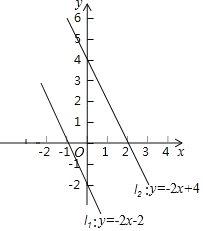
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
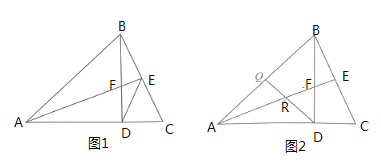
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)如图1,连结![]() ,问
,问![]() 是否为
是否为![]() 的平分线?请说明理由.
的平分线?请说明理由.
(3)如图2,![]() 为
为![]() 的中点,连结
的中点,连结![]() 交
交![]() 于
于![]() ,用等式表示
,用等式表示![]() 与
与![]() 的数量关系?并给出证明.
的数量关系?并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com