练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，点C在⊙O上，点P是圆上一动点，且与点C分别位于直径AB的两侧，，过点C作交PB的延长线于点Q；

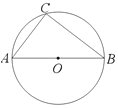
    (1)当点P运动到什么位置时，CQ恰好是⊙O的切线？

    (2)若点P与点C关于直径AB对称，且AB=5，求此时CQ的长．

    【答案】(1)当点P运动到直线OC与的交点处；(2)CQ=6.4.

    【解析】

    （1）根据切线的定义，直接判断即可；

    （2）根据tan∠CPB=tan∠A=，AB=5，求出AC，BC的长，在根据对称，利用等积法求出CP的长度，最后，再根据tan∠CPB=tan∠A== ，求出CQ的长即可．

    (1) 根据切线的定义，如图当点P运动到直线OC与的交点处，CQ恰好是⊙O的切线.

    (2)连接CB，∵是直径，.∵ ， ,∵， ， .∵点P与点C关于直径AB对称,.在中，，在中， .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示为二次函数的图象，在下列选项中错误的是（ ）

    A.

    B. 时，随的增大而增大

    C.

    D. 方程的根是，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】象棋是棋类益智游戏，中国象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的棋艺活动．李凯和张萌利用象棋棋盘和棋子做游戏．李凯将四枚棋子反面朝上放在棋盘上，其中有两个“兵”、一个“马”、一个“士”，张萌随机从这四枚棋子中摸一枚棋子，记下正汉字，然后再从剩下的三枚棋子中随机摸一枚．

    （1）求张萌第一次摸到的棋子正面上的汉字是“兵”的概率；

    （2）游戏规定：若张萌两次摸到的棋子中有“士”，则张萌胜；否则，李凯胜．请你用树状图或列表法求李凯胜的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线y=x+3与x轴交于点A，与y轴交于点B，抛物线y=a+bx+c(a<0)经过点A，B，

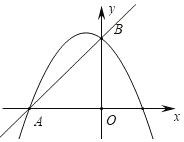
    (1)求a、b满足的关系式及c的值，

    (2)当x<0时，若y=a+bx+c(a<0)的函数值随x的增大而增大，求a的取值范围，

    (3)如图，当a=1时，在抛物线上是否存在点P，使△PAB的面积为?若存在，请求出符合条件的所有点P的坐标；若不存在，请说明理由，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y＝ax2＋bx＋c(a≠0)的图象经过点A，B，C．现有下面四个推断：①抛物线开口向下；②当x=－2时，y取最大值；③当m<4时，关于x的一元二次方程ax2＋bx＋c=m必有两个不相等的实数根；④直线y=kx+c(k≠0)经过点A，C，当kx+c> ax2＋bx＋c时，x的取值范围是－4<x<0；其中推断正确的是 （ ）

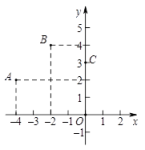
    A. ①②B. ①③C. ①③④D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠A=36°，AB=AC，BD平分∠ABC，则图中等腰三角形的个数是（ ）

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

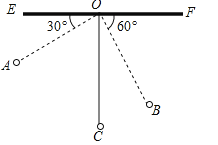
    【题目】（2017内蒙古通辽市）如图，物理教师为同学们演示单摆运动，单摆左右摆动中，在OA的位置时俯角∠EOA=30°，在OB的位置时俯角∠FOB=60°，若OC⊥EF，点A比点B高7cm．求：

    （1）单摆的长度（≈1.7）；

    （2）从点A摆动到点B经过的路径长（π≈3.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝﹣（x+1）（x﹣9）与坐标轴交于A、B、C三点，D为顶点，连结AC，BC．点P是该抛物线在第一象限内上的一点．过点P作y轴的平行线交BC于点E，连结AP交BC于点F，则的最大值为_______．

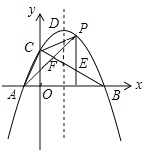
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题发现：

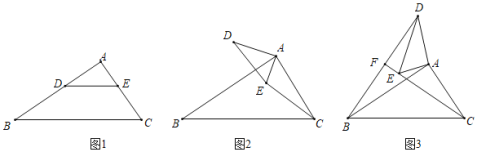
    (1)如图1，在Rt△ABC中，∠A＝90°，AB＝kAC(k＞1)，D是AB上一点，DE∥BC，则BD，EC的数量关系为　 　．

    类比探究

    (2)如图2，将△AED绕着点A顺时针旋转，旋转角为a(0°＜a＜90°)，连接CE，BD，请问(1)中BD，EC的数量关系还成立吗？说明理由

    拓展延伸：

    (3)如图3，在(2)的条件下，将△AED绕点A继续旋转，旋转角为a(a＞90°)．直线BD，CE交于F点，若AC＝1，AB＝，则当∠ACE＝15°时，BFCF的值为_____．

    查看答案和解析>>

    同步练习册答案