
 ���κ���y=x2+��2m+1��x+m2��ͼ��x����A��x1��0����B��x2��0������֪x1��x2��x12+x1•x2+x22=21��
���κ���y=x2+��2m+1��x+m2��ͼ��x����A��x1��0����B��x2��0������֪x1��x2��x12+x1•x2+x22=21������ ��1������������x��Ľ��������ϸ���ϵ���Ĺ�ϵ�ɵó�x1+x2=-2m-1��x1•x2=m2�����x12+x1•x2+x22=21���ɵó�����m��һԪ���η��̣��ⷽ�̼��ɵó�m��ֵ���ٸ���x1��x2��ϸ����б�ʽ�ɵó�����m��һԪһ�β���ʽ���ⲻ��ʽ���ɵó�m��ȡֵ��Χ���ɴ˼���ȷ��m��ֵ��
��2����m=2������κ�������ʽ������y=0�����������A��B�����꣬�����ɵó�AB�ij��������������ε������ʽ��ϡ�ABM�����Ϊ6���ɵó���M�������꣬���������κ�������ʽ�����xֵ���ٸ��ݡ�MABΪ��ǣ�����ȷ����M�����꣬���ݵ�A��M���������ô���ϵ�����������ֱ��AM�Ľ���ʽ��
��3���ӳ�AP��y���ڵ�C����A��M������ɵó���MAO=45�㣬���AP��AM���ɵó���C�����꣬�Ӷ��ó�ֱ��AC�Ľ���ʽ������ֱ��AC�������ߵĽ���ʽ�ɷ����飬�ⷽ���鼴�������P�����꣮������ڷ�������ĵ�Q�����Q������Ϊ��n��0�����ٷ֡�APQ�ס�AMB���AQP�ס�AMB����������ǣ��������������ε����ʼ����ҳ�����n��һԪһ�η��̣��ⷽ�̼������nֵ���Ӷ��ó���Q�����꣮
��� �⣺��1���߶��κ���y=x2+��2m+1��x+m2��ͼ��x����A��x1��0����B��x2��0����
��x1+x2=-2m-1��x1•x2=m2��
��x12+x1•x2+x22=$��{x}_{1}+{x}_{2}��^{2}$-x1•x2=3m2+4m+1=21��
��m1=-$\frac{10}{3}$��m2=2��
��x1��x2��
���=��2m+1��2-4m2=4m+1��0��
��m��-$\frac{1}{4}$��
��m��ֵΪ2��
��2����m=2��
����κ�������ʽΪy=x2+5x+4��
��y=0ʱ����x2+5x+4=��x+1����x+4��=0��
��ã�x1=-4��x2=-1��
��A��-4��0����B��-1��0����
��AB=3��
��S��ABM=$\frac{1}{2}$AB•|yM|=$\frac{1}{2}$��3��|yM|=6��
��yM=��4��
��y=4ʱ��x2+5x+4=4��
��ã�x1=-5��x2=0��
��ʱ��M��-5��4������0��4����
��y=-4ʱ��x2+5x+4=-4��
��=52-4��8=-7��0��
��ʱ�⣮
�ߡ�MABΪ��ǣ�
��M��0��4����
��ֱ��AM�Ľ���ʽΪy=kx+4��
����-4��0������y=kx+4��
�ã�0=-4k+4����ã�k=1��
��ֱ��AM�Ľ���ʽΪy=x+4��
��3���ӳ�AP��y���ڵ�C����ͼ��ʾ��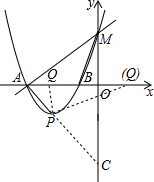
��A��-4��0����M��0��4����
���MAO=45�㣬
��AP��AM��
���CAO=45�㣬
��C��0��-4����ֱ��AC�Ľ���ʽΪy=-x-4��
����ֱ��AC�������߽���ʽ�ɷ�����ã�$\left\{\begin{array}{l}{y=-x-4}\\{y={x}^{2}+5x+4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$��$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$����ȥ����
��P��-2��-2����
��A��-4��0����M��0��4����B��-1��0����
��AM=4$\sqrt{2}$��AB=3��AP=2$\sqrt{2}$��
������ڷ�������ĵ�Q�����Q������Ϊ��n��0������AQ=|n+4|��
�ߡ�PAQ=��BAM=45�㣬
��AQ=n+4����A��P��QΪ��������������ABM���Ʒ����������
�ٵ���APQ�ס�AMBʱ����$\frac{AP}{AM}=\frac{AQ}{AB}$��
��$\frac{2\sqrt{2}}{4\sqrt{2}}=\frac{n+4}{3}$����ã�n=-$\frac{5}{2}$��
��ʱ��Q������Ϊ��-$\frac{5}{2}$��0����
�ڵ���AQP�ס�AMBʱ����$\frac{AQ}{AM}=\frac{AP}{AB}$��
��$\frac{n+4}{4\sqrt{2}}=\frac{2\sqrt{2}}{3}$����ã�n=$\frac{4}{3}$��
��ʱ��Q������Ϊ��$\frac{4}{3}$��0����
���Ͽ�֪����x���ϴ���һ��Q��ʹ����A��P��QΪ��������������ABM���ƣ���Q�����꣨-$\frac{5}{2}$��0����$\frac{4}{3}$��0����
���� ���⿼���˴���ϵ������������ʽ������ϵ���Ĺ�ϵ�������б�ʽ�Լ����������ε��ж������ʣ�����Ĺؼ��ǣ���1�����ø���ϵ���Ĺ�ϵ�ҳ�����m��һԪ���η��̣���2�������M�����ꣻ��3��������������ǣ����������е��⣬�ѶȲ������������Ŀʱ���������������ε������ҳ������֮��Ĺ�ϵ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�����һ��ֱ�������ε��ڽ������ε����ǡ���������������0.48�������ֱ�������ε�����ֱ�DZߵı�Ϊ��������
��ͼ�����һ��ֱ�������ε��ڽ������ε����ǡ���������������0.48�������ֱ�������ε�����ֱ�DZߵı�Ϊ��������| A�� | 1��2 | B�� | 2��3 | C�� | 3��4 | D�� | 4��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | -8 | B�� | -6 | C�� | -4 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| ��λ�����֣� | �������֣� | ����֣� | ƽ�������֣� | |
| ���꼶��1���� | 75 | 75 | 25 | 75 |
| ���꼶��2���� | 75 | 90 | 30 | 75 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������������һ����������һ����������ɣ�����ʽ��ʾ�����������������ָ�����Ĵ�����
��ͼ��ʾ������������һ����������һ����������ɣ�����ʽ��ʾ�����������������ָ�����Ĵ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D��BC�ϣ�BD=10��DC=8����DAC=��B��E��AB��һ�㣬��DE��AC����AC��DE�ij���
��ͼ���ڡ�ABC�У���D��BC�ϣ�BD=10��DC=8����DAC=��B��E��AB��һ�㣬��DE��AC����AC��DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com