
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 有无数个 |
分析 由题意求方程的解且要使x,y都是正整数,将方程移项将x和y互相表示出来,在由题意要求x>0,y>0根据以上两个条件可夹出合适的x值从而代入方程得到相应的y值.
解答 解:由题意求方程3x+y=9的解且要使x,y都是正整数,
∴y=9-3x>0,
∴x≤2,
又∵x≥0且x为正整数,
∴x值只能是x=1,2,代入方程得相应的y值为y=6,3.
∴方程3x+y=9的解是:$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
故选:B.
点评 本题是求不定方程的整数解,主要考查方程的移项,合并同类项,系数化为1等技能,先将方程做适当变形,确定其中一个未知数的取值范围,然后枚举出适合条件的所有整数值,再求出另一个未知数的值.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
| 部门 | 人数 | 每人所创年利润/万元 |
| A | 1 | 36 |
| B | 6 | 27 |
| C | 8 | 16 |
| D | 11 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要建一个如图所示的面积为300m2的长方形围栏,围栏总长50m,一边靠墙(墙长25m).
要建一个如图所示的面积为300m2的长方形围栏,围栏总长50m,一边靠墙(墙长25m).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{22}{3}$ | B. | $\frac{25}{6}$ | C. | $\frac{11}{4}$ | D. | $\frac{22}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
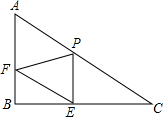 已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com