
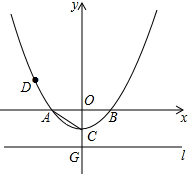
 如图,在以O为坐标原点的平面直角坐标系中,二次函数y=$\frac{1}{4}$x2+bx+c 的图象与x轴交于A,B两点,与y轴交于点C(0,-1).连结AC,tan∠OCA=2,直线l 过点G(0,-2)且平行于x轴.
如图,在以O为坐标原点的平面直角坐标系中,二次函数y=$\frac{1}{4}$x2+bx+c 的图象与x轴交于A,B两点,与y轴交于点C(0,-1).连结AC,tan∠OCA=2,直线l 过点G(0,-2)且平行于x轴.分析 (1)将点C的坐标代入二次函数解析式中可求出c值,在Rt△AOC中通过解直角三角形可求出点A的坐标,将其代入二次函数解析式中即可求出b值;
(2)①由二次函数图象上点的坐标特征可设点D(m,$\frac{1}{4}$m2-1),根据两点间的距离公式以及点到直线的距离可分别表示出OD和d的长度,比较后即可得出结论;
②过点D作DD′⊥直线l于点D′,过点E作EE′⊥直线l于点E′,连接OD、OE,取线段DE的中点M,过M作MM′⊥直线l于点M′,由①可得DD′=OD、EE′=OE,利用梯形的中位线可得出MM′=$\frac{1}{2}$(DD′+EE′),再利用三角形的三边关系即可得出DD′+EE′>DE,从而得出MM′>$\frac{1}{2}$DE,即以线段DE为直径的圆与直线l相离.
解答 解:(1)当x=0时,y=$\frac{1}{4}$x2+bx+c=c=-1,
∴c=-1;
∵点C(0,-1),tan∠OCA=2,
∴OA=2OC=2,
∴A(-2,0).
将A(-2,0)代入y=$\frac{1}{4}$x2+bx-1中,
0=1-2b-1,解得:b=0.
故答案为:0;-1.
(2)①d=DO恒成立,理由如下:
设点D(m,$\frac{1}{4}$m2-1),
∴d=$\frac{1}{4}$m2-1-(-2)=$\frac{1}{4}$m2+1,DO=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\sqrt{\frac{1}{16}{m}^{4}+\frac{1}{2}{m}^{2}+1}$=$\frac{1}{4}$m2+1,
∴d=DO.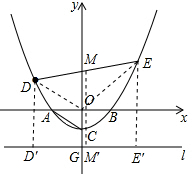 ②以线段DE为直径的圆与直线l相离,理由如下:
②以线段DE为直径的圆与直线l相离,理由如下:
过点D作DD′⊥直线l于点D′,过点E作EE′⊥直线l于点E′,连接OD、OE,取线段DE的中点M,过M作MM′⊥直线l于点M′,如图所示.
由①可知:DD′=OD,EE′=OE.
∵DD′⊥直线l,EE′⊥直线l,MM′⊥直线l,点M为线段DE的中点,
∴MM′为梯形DD′E′E的中位线,
∴MM′=$\frac{1}{2}$(DD′+EE′).
在△ODE中,OD+OE>DE,
∴DD′+EE′>DE,
∴MM′>$\frac{1}{2}$DE,
∴以线段DE为直径的圆与直线l相离.
点评 本题考查了待定系数法求二次函数解析式、解直角三角形、点到直线的距离、三角形三边关系以及梯形的中位线,解题的关键是:(1)根据点的坐标利用待定系数法求出b、c值;(2)①利用两点间的距离公式以及点到直线的距离可分别表示出OD和d的长度;②根据三角形三边关系结合①找出DD′+EE′>DE.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
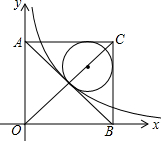 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(6-3$\sqrt{2}$)的圆内切于△ABC,则k的值为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com