
 如图,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,连接OC,过点A作AD∥OC交⊙O于点D,连接CD.
如图,在Rt△ABC中,∠ABC=90°,AB是⊙O的直径,连接OC,过点A作AD∥OC交⊙O于点D,连接CD.分析 (1)连接OD,易证∠OAD=∠ODA,由于OC∥AD,所以可证∠DOC=∠BOC,从而可证△OBC≌△ODC(SAS),所以∠ODC=90°.
(2)AD∥OC,所以$\frac{OA}{DC}=\frac{EA}{ED}$,可设OA=3a,DC=4a,所以BC=DC=4a,AB=6a,利用tan∠ACB=$\frac{AB}{BC}$即可求出答案.
解答 证明:(1)连接OD.
∵OA=OD,
∴∠OAD=∠ODA,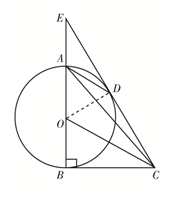
∵OC∥AD,
∴∠OAD=∠BOC,∠ADO=∠DOC,
∴∠DOC=∠BOC,
在△OBC与△ODC中,
$\left\{\begin{array}{l}{OD=OB}\\{∠DOC=∠BOC}\\{OC=OC}\end{array}\right.$
∴△OBC≌△ODC(SAS),
∴∠ODC=∠OBC=90°,
∴CD是⊙O的切线;
(2)∵AD∥OC,
∴$\frac{OA}{DC}=\frac{EA}{ED}=\frac{3}{4}$,
设OA=3a,DC=4a,
∵△OBC≌△ODC,
∴BC=DC=4a,
又∵AB=2OA=6a,
∴tan∠ACB=$\frac{AB}{BC}=\frac{6a}{4a}$=$\frac{3}{2}$
点评 本题考查圆的综合问题,涉及全等三角形的判定与性质,相似三角形的判定与性质,切线的判定,锐角三角函数等知识,综合程度较高,需要学生灵活运用知识.


科目:初中数学 来源: 题型:解答题
| 册数(x) | 1 | 2 | 3 | … | |
| 价格(y) | 7.5 | 15 | 30 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
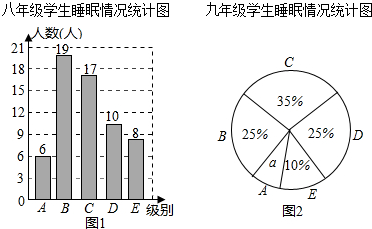
| 组别 | 睡眠时间x |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
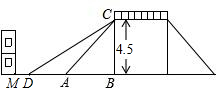 如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)
如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
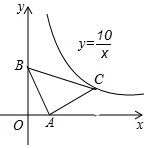 如图,在△ABC中,AB=AC,∠BAC=90°,点A在x轴上,点B的坐标是(0,3),若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,那么点C的坐标为(5,2).
如图,在△ABC中,AB=AC,∠BAC=90°,点A在x轴上,点B的坐标是(0,3),若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,那么点C的坐标为(5,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
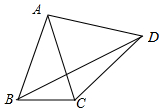 如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$.
如图,△ABC中,AB=AC=5,BC=2,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD=$\sqrt{3}$+2$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )| A. | ∠3=58° | B. | ∠4=122° | C. | ∠5=52° | D. | ∠2=58° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com