
【题目】一次函数y=ax+a(a为常数,a≠0)与反比例函数y= ![]() (a为常数,a≠0)在同一平面直角坐标系内的图象大致为( )
(a为常数,a≠0)在同一平面直角坐标系内的图象大致为( )
A.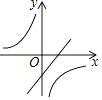
B.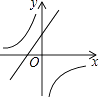
C.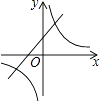
D.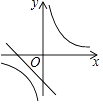
【答案】C
【解析】当a>0时,一次函数y=ax+a,经过一二三象限,反比例函数图象位于一、三象限,
当a<0时,一次函数y=ax+a,经过二、三、四象限,反比例函数图象位于二、四象限.
所以答案是:C.
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识,掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远,以及对反比例函数的图象的理解,了解反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


科目:初中数学 来源: 题型:
【题目】综合题
(1)阅读理解:如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB、AD、DC之间的等量关系为;
(2)问题探究:如图②,在四边形ABCD中,AB∥DC,AF与DC的延长线交于点F,E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.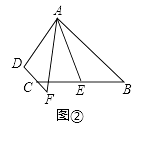
(3)问题解决:如图③,AB∥CF,AE与BC交于点E,BE:EC=2:3,点D在线段AE上,且∠EDF=∠BAE,试判断AB、DF、CF之间的数量关系,并证明你的结论.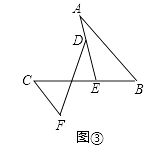
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2017年张学友演唱会”于6月3日在我市观山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
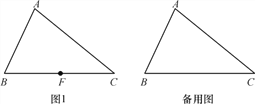
【题目】已知三角形ABC,EF∥AC交直线AB于点E,DF∥AB交直线AC于点D.
(1)如图1,若点F在边BC上,
①补全图形;
②判断∠BAC与∠EFD的数量关系,并给予证明;
(2)若点F在边BC的延长线上,(1)中的结论还成立吗?若成立,给予证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:

(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则△BDE的面积的最小值为 . 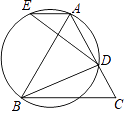
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com