
【题目】鹿山广场元旦期间搞促销活动,如图.

(1)小哲在促销活动时两次购物分别用了135元和481元.
①若小哲购物时没有促销活动,则他共需付多少钱?
②若你需购这些同样的物品,请问还有更便宜的购物方案吗?若有,请说出购物方案,并算出共需付多少钱;若没有,则说明理由.
(2)若小明购了原价为a元的物品,小红购了原价为b元的物品,且a<b,但最后小明所付的钱反而比小红多.
①你列举一对a,b的值;
②求符合条件的整数a,b共有几对?(直接答案即可).
【答案】(1)①若小哲购物时没有促销活动,则他共需付720元;②购物方案是两次购物合并成为一次,共需付钱601元;(2)①见解析;②符合条件的整数a、b共有66对.
【解析】
(1)①根据购物不超过200元优惠10%打九折和超过200元而不超过500元全部优惠15%打8.5折可列方程求解即可;
②还有更便宜的购物方案,购物方案是两次购物合并成为一次,按照不同购买金额乘以对应的折扣并相加可以得出共需付的钱数;
(2)①可选取大小比较接近,但处于不同优惠范围的数值即可;
②由题意得:(1-15%)b<200×(1-10%)而(1-10%)a>200×(1-15%),且a≤200<b,故200<b≤![]() ,
,![]() <a≤200,从而符合条件的整数a有189~200,整数b有201~211,分别对b和a取值计算,最后把符合条件的整数个数相加即可.
<a≤200,从而符合条件的整数a有189~200,整数b有201~211,分别对b和a取值计算,最后把符合条件的整数个数相加即可.
(1)①小哲在促销活动时购物用了135元,则原价为135÷(1﹣10%)=150元;
小哲在促销活动时购物用了481元,设原价为x元,由题意得:
500×(1﹣15%)+(1﹣20%)(x﹣500)=481,
解得:x=570,
若小哲购物时没有促销活动,则150+570=720(元),
答:若小哲购物时没有促销活动,则他共需付720元;
②若我需购买这些同样的物品,则还有更便宜的购物方案,购物方案是两次购物合并成为一次,共需付钱:
500×(1﹣15%)+(1﹣20%)×(720﹣500)=425+176=601(元).
(2)①若小明购了原价为a元的物品,小红购了原价为b元的物品,且a<b,但最后小明所付的钱反而比小红多.
列举一对a、b的值为a=190,b=201,
当a=190时,实际付款190×(1﹣10%)=171(元),
而b=201时,实际付款201×(1﹣15%)=170.85(元).
②由题意得:(1﹣15%)b<200×(1﹣10%),
而(1﹣10%)a>200×(1﹣15%),且a≤200<b,
∴200<b≤![]() ,
,![]() <a≤200,
<a≤200,
∴符合条件的整数a有189~200,整数b有201~211,
若a=189,则0.85b<189×0.9,b<![]() ,没有满足条件的整数b;
,没有满足条件的整数b;
若a=190,则0.85b<190×0.9,b<![]() ,满足条件的整数b为b=201;
,满足条件的整数b为b=201;
若a=191,则0.85b<191×0.9,b<![]() ,满足条件的整数b有:201,202;
,满足条件的整数b有:201,202;
若a=192,则0.85b<192×0.9,b<![]() ,满足条件的整数b有:201,202,203;
,满足条件的整数b有:201,202,203;
若a=193,则0.85b<193×0.9,b<![]() ,满足条件的整数b有:201,202,203,204;
,满足条件的整数b有:201,202,203,204;
若a=194,则0.85b<194×0.9,b<![]() ,满足条件的整数b有:201,202,203,204,205;
,满足条件的整数b有:201,202,203,204,205;
…
若a=200,则0.85b<200×0.9,b<![]() ,满足条件的整数b有:201,202,203,204,205,206,207,208,209,210,211;
,满足条件的整数b有:201,202,203,204,205,206,207,208,209,210,211;
∴符合条件的整数a、b共有:1+2+3+4+5+6+7+8+9+10+11=66(对).


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
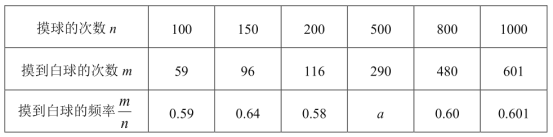
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织部分师生从学校(A地)到300千米外的B地进行红色之旅(革命传统教育),租用了客运公司甲、乙两辆车,其中乙车速度是甲车速度的![]() ,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
,两车同时从学校出发,以各自的速度匀速行驶,行驶2小时后甲车到达服务区C地,此时两车相距40千米,甲车在服务区休息15分钟户按原速度开往B地,乙车行驶过程中未做停留.
(1)求甲、乙两车的速度?
(2)问甲车在C地结束休息后再行驶多长时间,甲、乙两车相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
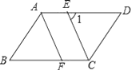
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC 中,∠ACB=90°,BC=2,AC=3,以点C为圆心、CB为半径的圆交AB于点D,过点A作AE∥CD,交BC延长线于点E.
(1)求CE的长;
(2)P是 CE延长线上一点,直线AP、CD交于点Q.
①如果△ACQ ∽△CPQ,求CP的长;
②如果以点A为圆心,AQ为半径的圆与⊙C相切,求CP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
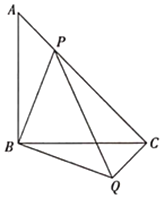
【题目】如图,等腰直角![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,将
上,将![]() 绕顶点
绕顶点![]() 沿顺时针方向旋转90°后得到
沿顺时针方向旋转90°后得到![]() .
.
(1)求![]() 的度数;
的度数;
(2)当![]() ,
,![]() 时,求
时,求![]() 的大小;
的大小;
(3)当点![]() 在线段
在线段![]() 上运动时(
上运动时(![]() 不与
不与![]() ,
,![]() 重合),求证:
重合),求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
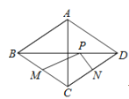
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com