
分析 设三角形△ABC,由勾股定理可求得直角三角形的斜边,设内切圆的半径为r,由S△ABC=$\frac{1}{2}$(AB+BC+CA)•r可求得半径,则可求得直径.
解答 解:
设三角形为△ABC,∠C=90°,AC=8,BC=15,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+1{5}^{2}}$=17,
设内切圆的半径为r,则S△ABC=$\frac{1}{2}$(AB+BC+CA)•r,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$(AB+BC+CA)•r,即$\frac{1}{2}$×8×15=$\frac{1}{2}$×(8+15+17)•r,
解得r=3,
∴内切圆的直径是6步,
故答案为:6.
点评 本题主要考查三角形的内切圆,利用等积法得到关于内切圆半径的方程是解题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
 如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称
如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称查看答案和解析>>
科目:初中数学 来源: 题型:填空题
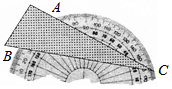 将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.
将一个三角形纸板按如图所示的方式放置一个破损的量角器上,使点C落在半圆上,若点A、B处的读数分别为65°、20°,则∠ACB的大小为22.5°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
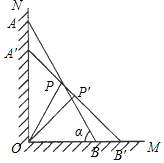 如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.
如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com