
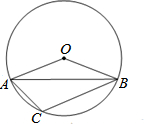
 如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°.
如图,在⊙O中,已知∠OAB=21.5°,则∠C的度数为111.5°.  一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
阅读材料,如图,在平面直角坐标系中,O为坐标原点,对于任意两点A(x1,y1),B(x2,y2).由勾股定理可得:AB2=(x1-x2)2+(y1-y2)2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A,B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF.
如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 国外品牌 | 国内品牌 | |
| 进价(元/部) | 4400 | 2000 |
| 售价(元/部) | 5000 | 2500 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com