
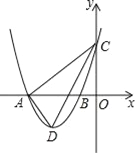
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+3гыxжсНЛгкAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈЉlЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧЕкШ§ЯѓЯоЕФХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуDЕФКсзјБъЮЊmЃЌЁїACDЕФУцЛ§ЮЊСПЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂШЗЖЈmЮЊКЮжЕЪБSгазюДѓжЕЃЌзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉШєЕуPЪЧХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЪЧЗёДцдкЕуPЪЙЕУЁЯAPC=90ЁуЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=![]() x2+
x2+![]() x+3ЃЛЃЈ2ЃЉmЮЊЉ2ЪБSгазюДѓжЕЃЌзюДѓжЕЪЧ6ЃЈ3ЃЉPЕФзјБъЮЊЃЈЉ
x+3ЃЛЃЈ2ЃЉmЮЊЉ2ЪБSгазюДѓжЕЃЌзюДѓжЕЪЧ6ЃЈ3ЃЉPЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ ![]() ЃЉ
ЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)ЁЂНЋЕуAКЭЕуBЕФзјБъДњШыНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЛ(2)ЁЂЪзЯШЧѓГіЕуCЕФзјБъЃЌШЛКѓРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпACЕФКЏЪ§НтЮіЪНЃЌЙ§ЕуD DзїDEЁЮyжсЃЌНЛACгкЕуEЃЌЩшГіЕуDКЭЕуEЕФзјБъЃЌШЛКѓЧѓГіDEЕФГЄЖШЃЌИљОнУцЛ§ЕФМЦЫуЙЋЪНЕУГіУцЛ§ЕФЖўДЮКЏЪ§НтЮіЪНЃЌДгЖјЕУГіУцЛ§ЕФзюДѓжЕЃЛ(3)ЁЂвдACЮЊжБОЖзїдВНЛХзЮяЯпЕФЖдГЦжсгкPЃЌИљОнЕуA КЭЕуCЕФзјБъЕУГіжаЕуЕФзјБъЃЌЧѓГіACКЭOPЕФГЄЖШЃЌЩшЕуPЕФзјБъЮЊЃЈ![]() ЃЌyЃЉЃЌШЛКѓИљОнЙДЙЩЖЈРэЧѓГіyЕФжЕЃЌЕУГіЕуPЕФзјБъЃЎ
ЃЌyЃЉЃЌШЛКѓИљОнЙДЙЩЖЈРэЧѓГіyЕФжЕЃЌЕУГіЕуPЕФзјБъЃЎ
ЪдЬтНтЮіЃК(1)ЁЂНЋAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈЉlЃЌ0ЃЉДњШыy=ax2+bx+3ЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ ЙЪХзЮяЯпЕФКЏЪ§НтЮіЪНЮЊy=
ЃЌ ЙЪХзЮяЯпЕФКЏЪ§НтЮіЪНЮЊy=![]() x2+
x2+![]() x+3ЃЛ
x+3ЃЛ
(2)ЁЂСюx=0ЃЌдђy=3ЃЌ ЁрCЃЈ0ЃЌ3ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊy=mx+nЃЌ ДњШыAЃЈЉ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉЕУ![]() ЃЌ НтЕУ
ЃЌ НтЕУ![]()
ЁрACЕФНтЮіЪНЮЊy=![]() x+3ЃЛ
x+3ЃЛ
Й§DзїDEЁЮyжсЃЌНЛACгкЕуEЃЌЩшDЃЈmЃЌ![]() m2+
m2+![]() m+3ЃЉЃЌEЃЈmЃЌ
m+3ЃЉЃЌEЃЈmЃЌ![]() m+3ЃЉЃЈЉ4ЃМmЃМЉ1ЃЉЃЌ дђDE=
m+3ЃЉЃЈЉ4ЃМmЃМЉ1ЃЉЃЌ дђDE=![]() m+3ЉЃЈ
m+3ЉЃЈ![]() m2+
m2+![]() m+3ЃЉЃЌ ЁрDE=Љ
m+3ЃЉЃЌ ЁрDE=Љ![]() m2Љ3mЃЌ
m2Љ3mЃЌ
ЁрS=![]() DEЁС4=2ЃЈЉ
DEЁС4=2ЃЈЉ![]() m2Љ3mЃЉ=Љ
m2Љ3mЃЉ=Љ![]() m2Љ6m=Љ
m2Љ6m=Љ![]() ЃЈm+2ЃЉ2+6ЃЌ
ЃЈm+2ЃЉ2+6ЃЌ
Ёрm=Љ2ЪБЃЌSзюДѓ=6ЃЛ ЙЪmЮЊЉ2ЪБSгазюДѓжЕЃЌзюДѓжЕЪЧ6ЃЎ
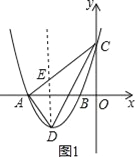
(3)ЁЂДцдкЕуPЪЙЕУЁЯAPC=90ЁуЃЌ вдACЮЊжБОЖзїдВНЛХзЮяЯпЕФЖдГЦжсгкPЃЌ
ЁпAЃЈЉ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉЃЌ ЁрACЕФжаЕуOЕФзјБъЮЊЃЈЉ2ЃЌ![]() ЃЉЃЌAC=
ЃЉЃЌAC=![]() =5ЃЌ
=5ЃЌ
ЁрOP=![]() =
=![]() ЃЌ ЁпХзЮяЯпy=ax2+bx+3гыxжсНЛгкAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈЉlЃЌ0ЃЉСНЕуЃЌ
ЃЌ ЁпХзЮяЯпy=ax2+bx+3гыxжсНЛгкAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈЉlЃЌ0ЃЉСНЕуЃЌ
ЁрЖдГЦжсx=![]() =Љ
=Љ![]() ЃЌ ЩшPЃЈЉ
ЃЌ ЩшPЃЈЉ![]() ЃЌyЃЉЃЌ ЁрOP2=ЃЈ
ЃЌyЃЉЃЌ ЁрOP2=ЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
МДЃЈЉ2+![]() ЃЉ2+ЃЈ
ЃЉ2+ЃЈ![]() ЉyЃЉ2=ЃЈ
ЉyЃЉ2=ЃЈ![]() ЃЉ2ЃЌ НтЕУy=
ЃЉ2ЃЌ НтЕУy=![]() ЁР
ЁР![]() ЃЌ
ЃЌ
ЁрPЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЬсГі
ФГЩЬЕъОЯњЁЖГЌФмТНеНЖгЁЗГЌУШЁАаЁАзЁБЃЈЭМ1ЃЉЭцОпЃЌЁАаЁАзЁБЭцОпУПИіНјМл60дЊЃЎЮЊНјааДйЯњЃЌЩЬЕъжЦЖЈШчЯТЁАгХЛнЁБЗНАИЃКШчЙћвЛДЮЯњЪлЪ§СПВЛГЌЙ§10ИіЃЌдђЯњЪлЕЅМлЮЊ100дЊ/ИіЃЛШчЙћвЛДЮЯњЪлЪ§СПГЌЙ§10ИіЃЌУПдіМгвЛИіЃЌЫљгаЁАаЁАзЁБЭцОпЯњЪлЕЅМлНЕЕЭ1дЊ/ИіЃЌЕЋЕЅМлВЛЕУЕЭгк80дЊ/ИіЃЎвЛДЮЯњЪлЁАаЁАзЁБЭцОпЕФЕЅМлyЃЈдЊ/ИіЃЉгыЯњЪлЪ§СПxЃЈИіЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЎ

ЃЈ1ЃЉЧѓmЕФжЕВЂНтЪЭЩфЯпBCЫљБэЪОЕФЪЕМЪвтвхЃЛ
ЃЈ2ЃЉаДГіИУЕъЕБвЛДЮЯњЪлxИіЪБЃЌЫљЛёРћШѓwЃЈдЊЃЉгыxЃЈИіЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЕъГЄОЙ§вЛЖЮЪБМфЕФЯњЪлЗЂЯжЃКМДВЂВЛЪЧЯњСПдНДѓРћШѓдНДѓЃЈБШШчЃЌТє25ИізЌЕФЧЎЗДЖјБШТє30ИізЌЕФЧЎЖрЃЉЃЎЮЊСЫВЛГіЯжетжжЯжЯѓЃЌдкЦфЫћЬѕМўВЛБфЕФЧщПіЯТЃЌЕъГЄгІАбдРДЕФзюЕЭЕЅМл80ЃЈдЊ/ИіЃЉжСЩйЬсИпЕНЖрЩйдЊ/ИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЪЧЕШбќжБНЧЁїABCЭтвЛЕуЃЌАбBPШЦЕуBЫГЪБеыа§зЊ90ЁуЕНBPЁфЃЌвбжЊЁЯAPЁфBЃН135ЁуЃЌPЁфAЁУPЁфCЃН1ЁУ3ЃЌдђPЁфAЁУPBЃН( )

A. 1ЁУ![]() B. 1ЁУ2 C.
B. 1ЁУ2 C. ![]() ЁУ2 D. 1ЁУ
ЁУ2 D. 1ЁУ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
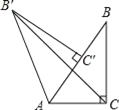
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЁЯBAC=60ЁуЃЌAB=2ЃЎRtЁїABЁфCЁфПЩвдПДзїЪЧгЩRtЁїABCШЦAЕуФцЪБеыЗНЯђа§зЊ60ЁуЕУЕНЕФЃЌЧѓЯпЖЮ BЁфCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙЁАЮвзюЯВАЎЕФвЛЯюЬхг§ЛюЖЏЁБЕїВщЃЌвЊЧѓУПУћбЇЩњБибЁЧвжЛФмбЁвЛЯюЃЌЯжЫцЛњГщВщСЫmУћбЇЩњЃЌВЂНЋЦфНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЬѕаЮЭМКЭЩШаЮЭМЃЎ

ЧыНсКЯвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉm= ЃЛ
ЃЈ2ЃЉЧыВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉдкЭМ2жаЃЌЁАЦЙХвЧђЁБЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ ЃЛ
ЃЈ4ЃЉвбжЊИУаЃЙВга1200УћбЇЩњЃЌЧыФуЙРМЦИУаЃдМга УћбЇЩњзюЯВАЎзуЧђЛюЖЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
аЁЮАгіЕНетбљвЛИіЮЪЬтЃКШчЭМ1ЃЌдке§Ш§НЧаЮABCФкгавЛЕуPЃЌЧвPA=3ЃЌPB=4ЃЌPC=5ЃЌЧѓЁЯAPBЕФЖШЪ§ЃЎ
аЁЮАЪЧетбљЫМПМЕФЃКШчЭМ2ЃЌРћгУа§зЊКЭШЋЕШЕФжЊЪЖЙЙдьЁїAPЁфCЃЌСЌНгPPЁфЃЌЕУЕНСНИіЬиЪтЕФШ§НЧаЮЃЌДгЖјНЋЮЪЬтНтОіЃЎ
ЧыФуЛиД№ЃКЭМ1жаЁЯAPBЕФЖШЪ§ЕШгкЁЁ ЁЁЃЎ
ВЮПМаЁЮАЭЌбЇЫМПМЮЪЬтЕФЗНЗЈЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉШчЭМ3ЃЌдке§ЗНаЮABCDФкгавЛЕуPЃЌЧвPA=![]() ЃЌPB=1ЃЌPD=
ЃЌPB=1ЃЌPD=![]() ЃЌдђЁЯAPBЕФЖШЪ§ЕШгкЁЁ ЁЁЃЌе§ЗНаЮЕФБпГЄЮЊЁЁ ЁЁЃЛ
ЃЌдђЁЯAPBЕФЖШЪ§ЕШгкЁЁ ЁЁЃЌе§ЗНаЮЕФБпГЄЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ4ЃЌдке§СљБпаЮABCDEFФкгавЛЕуPЃЌЧвPA=2ЃЌPB=1ЃЌPF=![]() ЃЌдђЁЯAPBЕФЖШЪ§ЕШгкЁЁ ЁЁЃЌе§СљБпаЮЕФБпГЄЮЊЁЁ ЁЁЃЎ
ЃЌдђЁЯAPBЕФЖШЪ§ЕШгкЁЁ ЁЁЃЌе§СљБпаЮЕФБпГЄЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy1=aЃЈx+2ЃЉ2Љ3гыy2=![]() ЃЈxЉ3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЃЈxЉ3ЃЉ2+1НЛгкЕуAЃЈ1ЃЌ3ЃЉЃЌЙ§ЕуAзїxжсЕФЦНааЯпЃЌЗжБ№НЛСНЬѕХзЮяЯпгкЕуBЃЌCЃЎдђвдЯТНсТлЃК
ЂйЮоТлxШЁКЮжЕЃЌy2ЕФжЕзмЪЧе§Ъ§ЃЛ
Ђкa=1ЃЛ
ЂлЕБx=0ЪБЃЌy2Љy1=4ЃЛ
Ђм2AB=3ACЃЛ
Цфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂк B. ЂкЂл C. ЂлЂм D. ЂйЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
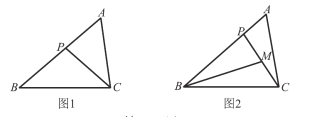
ЁОЬтФПЁПдкЁїABCжаЃЌPЮЊБпABЩЯвЛЕуЃЎ
(1)ШчЭМlЃЌШєЁЯACP=ЁЯBЃЌЧѓжЄЃКAC2 =APЁЄABЃЛ
(2)ШєMЮЊCPЕФжаЕуЃЌAC=2ЃЌШчЭМ2ЃЌШєЁЯPBM=ЁЯACPЃЌAB=3ЃЌЧѓBPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЪЪЕБЕФЗНЗЈНтЯТСаЗНГЬЃЎ
ЃЈ1ЃЉx2ЉxЉ1=0ЃЛ
ЃЈ2ЃЉx2Љ2x=2x+1ЃЛ
ЃЈ3ЃЉxЃЈxЉ2ЃЉЉ3x2=Љ1ЃЛ
ЃЈ4ЃЉЃЈx+3ЃЉ2=ЃЈ1Љ2xЃЉ2ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com