
【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
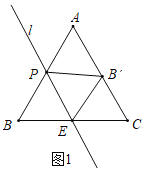
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
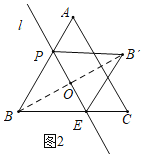
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
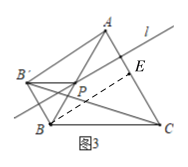
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
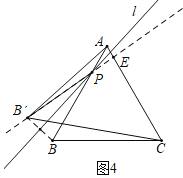
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

【答案】(1)4;(2)5![]() ;(3)面积不变,S△ACB’=
;(3)面积不变,S△ACB’=![]() ;(4)24+4
;(4)24+4![]()
【解析】
(1)证明△APB′是等边三角形即可解决问题;
(2)如图2中,设直线l交BC于点E,连接B B′交PE于O,证明△PEB是等边三角形,求出OB即可解决问题;
(3)如图3中,结论:面积不变,证明B B′//AC即可;
(4)如图4中,当PB′⊥AC时,△ACB′的面积最大,设直线PB′交AC于点E,求出B′E即可解决问题.
(1)如图1,∵△ABC为等边三角形,
∴∠A=60°,AB=BC=CA=8,
∵PB=4,
∴PB′=PB=PA=4,
∵∠A=60°,
∴△APB′是等边三角形,
∴AB′=AP=4,
故答案为:4;
(2)如图2,设直线l交BC于点E,连接B B′交PE于O,
∵PE∥AC,
∴∠BPE=∠A=60°,∠BEP=∠C=60°,
∴△PEB是等边三角形,
∵PB=5,B、B′关于PE对称,
∴BB′⊥PE,BB′=2OB,
∴OB=PB·sin60°=![]() ,
,
∴BB′=5![]() ,
,
故答案为:5![]() ;
;
(3)如图3,结论:面积不变.
过点B作BE⊥AC于E,
则有BE=AB·sin60°=![]() ,
,
∴S△ABC=![]() =16
=16![]() ,
,
∵B、B′关于直线l对称,
∴BB′⊥直线l,
∵直线l⊥AC,
∴AC//BB′,
∴S△ACB’=S△ABC=16![]() ;
;
(4)如图4,当B′P⊥AC时,△ACB′的面积最大,
设直线PB′交AC于E,
在Rt△APE中,PA=2,∠PAE=60°,
∴PE=PA·sin60°=![]() ,
,
∴B′E=B′P+PE=6+![]() ,
,
∴S△ACB最大值=![]() ×(6+
×(6+![]() )×8=24+4
)×8=24+4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,若点![]() 是线段
是线段![]() 上的动点(
上的动点(![]() 不与
不与![]() ,
,![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边向线段
为边向线段![]() 的同一侧作等边
的同一侧作等边![]() 和等边
和等边![]() .
.

(1)图1中,连接![]() 、
、![]() ,相交于点
,相交于点![]() ,设
,设![]() ,那么
,那么![]()
![]() ;
;
(2)如图2,若点![]() 固定,将
固定,将![]() 绕点
绕点![]() 按顺时针方向旋转(旋转角小于
按顺时针方向旋转(旋转角小于![]() ),此时
),此时![]() 的大小是否发生变化?请说明理由.
的大小是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+4与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式;
(3)y轴上是否存在一点P,使得S△PAB=![]() ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点B,D分别向线段AE作垂线段BQ和DF,点Q和F是垂足,连结AB,DE,BD,BD交AE于点C,且AB=DE,AF=EQ.

(1)求证:△ABQ≌△EDF;
(2)求证:C是BD的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AC为直径,弧AE=弧BD,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BCE;
(2)求证:BE是⊙O的切线;
(3)若EC=1,CD=3,求cos∠DBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点O为坐标原点,直线y=-x+4与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)在直线AB上是否存在点P,使△OAP是以OA为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若将Rt△AOB折叠,使OB边落在AB上,点O与点D重合,折痕为BC,求点C的坐标。
(4)直接写出折痕BC所在直线的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形置于平面直角坐标系第一象限,使AB边落在x轴正半轴上,且点A的坐标是(1,0).

(1)直线y=![]() x﹣
x﹣![]() 经过点C,且与x轴交于点E,求四边形AECD的面积;
经过点C,且与x轴交于点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com