
分析 (1)求出抛物线的对称轴,再根据对称性求出点B的坐标,然后求出点C的坐标,再把点A、C的坐标代入抛物线求出a、c即可得解;
(2)如图所示过点P作PD⊥AB,垂足为D.由点A、C的坐标先求得抛物线的解析式,然后再求得点P的坐标,从而可证明∠PBC=90°,然后求得PB的长度即可.
解答 解:(1)抛物线的对称轴为直线x=-$\frac{-4a}{2a}$=2,
∵点A(1,0),
∴点B的坐标为(3,0).
∵点C在y轴的负半轴,OB=OC,
∴点C的坐标为(0,-3).
(2)如图所示:过点P作PD⊥AB,垂足为D.
将点A和点C的坐标代入得:$\left\{\begin{array}{l}{a+c=0}\\{4a+c=-3}\end{array}\right.$
解得;a=-1.c=1.
∴抛物线的解析式为y=-x2+4x-3.
将x=2代入得:y=1.
∴顶点P的坐标为(2,1).
∴PD=BD=1.
∴∠DPB=∠DBP=45°.
∵OB=OC,∠COB=90°,
∴∠OBC=∠BCO=45°.
∴∠PBC=90°.
在Rt△PBD中,PB=$\sqrt{P{D}^{2}+B{D}^{2}}=\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
∴点P到BC的距离为$\sqrt{2}$.
点评 本题主要考查的是抛物线与x轴的交点,证得∠PBC=90°是解题的关键.


科目:初中数学 来源: 题型:解答题
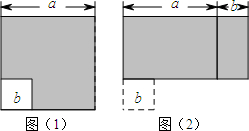 如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.
如图(1)所示,边长为a的大正方形中有一个边长为b的小正方形,如图(2)是由图(1)中阴影部分拼成的一个长方形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一菜农要修建一个育苗棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜45m2.
如图,一菜农要修建一个育苗棚,棚宽BE=2m,棚高AE=1.5m,长BC=18m.AE所在的墙面与地面垂直,现要在棚顶覆盖一种农用塑料薄膜,请你为他计算一下,共需多少这种塑料薄膜45m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
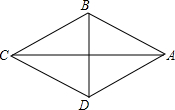 如图,在四边形ABCD中,AB与AD关于AC对称,给出下列结论:①BD是线段CA的垂直平分线;②CA平分∠BCD.其中( )
如图,在四边形ABCD中,AB与AD关于AC对称,给出下列结论:①BD是线段CA的垂直平分线;②CA平分∠BCD.其中( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①②都正确 | D. | ①②都不正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
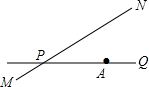 如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.
如图,公路PQ和公路MN交于点P,且∠NPQ=30°,公路PQ上有一所学校A,AP=160米.若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响,假设拖拉机行驶时周围100米以内会受到噪声的影响;则造成影响的时间为$\frac{20}{3}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
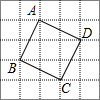 在如图的5×5网格中,小方格的边长为1.
在如图的5×5网格中,小方格的边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
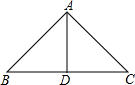 如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS.
如图,如果AD是BC边上的高,又是∠BAC的平分线,那么△ABD≌△ACD,其根据是ASA;如果AD是BC边上的高,又是BC边上的中线,那么△ABD≌△ACD,其根据是SAS.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com