
求出 的最小值.
的最小值.
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源:2012届初中毕业生学业考试(湖北黄石卷)数学(带解析) 题型:解答题
已知抛物线 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线 经过点
经过点
【小题1】求抛物线 的顶点坐标
的顶点坐标
【小题2】已知实数 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
.
【小题3】若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线 ,设
,设 用含有
用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的最小值及
的最小值及 取最小值时一次函数
取最小值时一次函数 的函数解析式。
的函数解析式。
(参考公式:在平面直角坐标系中,若 ,则
,则 ,
, 两点间的距离为)
两点间的距离为)
查看答案和解析>>
科目:初中数学 来源:2013届江苏省仪征市九年级第二次模拟考试数学试卷(带解析) 题型:解答题
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点 重合),点
重合),点 、
、 (
( )、
)、 在同一条直线上.
在同一条直线上. ,
, ,
,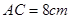 ,
, ,
, .如图(2),
.如图(2), 从图(1)的位置出发,以
从图(1)的位置出发,以 的速度沿
的速度沿 向
向 匀速移动,在
匀速移动,在 移动的同时,点
移动的同时,点 从
从 的顶点
的顶点 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿 向点
向点 匀速移动.当
匀速移动.当 的顶点
的顶点 移动到
移动到 边上时,
边上时, 停止移动,点
停止移动,点 也随之停止移动.
也随之停止移动. 与
与 相交于点
相交于点 ,连接
,连接 ,设移动时间为
,设移动时间为
 .
.

(1)当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻 ,使面积
,使面积 最小?若存在,求出
最小?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻 ,使
,使 、
、 、
、 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)
查看答案和解析>>
科目:初中数学 来源:2013届江苏省泰州市永安初级中学九年级下学期第二次涂卡训练数学试卷(带解析) 题型:解答题
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点 重合),点
重合),点 、
、 (
( )、
)、 在同一条直线上.
在同一条直线上. ,
, ,
, ,
, ,
, .如图(2),
.如图(2), 从图(1)的位置出发,以
从图(1)的位置出发,以 的速度沿
的速度沿 向
向 匀速移动,在
匀速移动,在 移动的同时,点
移动的同时,点 从
从 的顶点
的顶点 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿 向点
向点 匀速移动.当
匀速移动.当 的顶点
的顶点 移动到
移动到 边上时,
边上时, 停止移动,点
停止移动,点 也随之停止移动.
也随之停止移动. 与
与 相交于点
相交于点 ,连接
,连接 ,设移动时间为
,设移动时间为
 .
.
(1)当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻 ,使面积
,使面积 最小?若存在,求出
最小?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻 ,使
,使 、
、 、
、 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省仪征市九年级第二次模拟考试数学试卷(解析版) 题型:解答题
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点 重合),点
重合),点 、
、 (
( )、
)、 在同一条直线上.
在同一条直线上. ,
, ,
, ,
, ,
, .如图(2),
.如图(2), 从图(1)的位置出发,以
从图(1)的位置出发,以 的速度沿
的速度沿 向
向 匀速移动,在
匀速移动,在 移动的同时,点
移动的同时,点 从
从 的顶点
的顶点 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿 向点
向点 匀速移动.当
匀速移动.当 的顶点
的顶点 移动到
移动到 边上时,
边上时, 停止移动,点
停止移动,点 也随之停止移动.
也随之停止移动. 与
与 相交于点
相交于点 ,连接
,连接 ,设移动时间为
,设移动时间为
 .
.


(1)当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻 ,使面积
,使面积 最小?若存在,求出
最小?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻 ,使
,使 、
、 、
、 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北黄石初中毕业生学业考试数学试卷(解析版) 题型:解答题
已知抛物线 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线 经过点
经过点

1.求抛物线 的顶点坐标
的顶点坐标
2.已知实数 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
.
3.若抛物线先向上平移4个单位,再向左平移1个单位后得到抛物线 ,设
,设
 用含有
用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的最小值及
的最小值及 取最小值时一次函数
取最小值时一次函数 的函数解析式。
的函数解析式。
(参考公式:在平面直角坐标系中,若 ,则
,则 ,
, 两点间的距离为)
两点间的距离为)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com