
【题目】如图所示,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于D点. 求证:AC是⊙O的切线.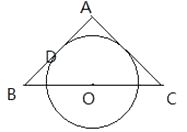
【答案】证明:过点O作OE⊥AC,垂足为E,连接OD,OA,
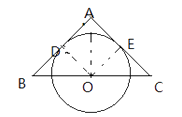
∵⊙O与AB相切于点D
∴OD⊥AB 又△ABC为
等腰三角形,O为底边BC的中点
∴AO是∠BAC的平分线
∴OE=OD,即OE是⊙O的半径
∴AC是⊙O的切线,得证.
【解析】证明一条直线是圆的切线的添加辅助线的方法:连半径,证垂直;作垂线,证半径。抓住关键的已知条件腰AB与⊙O相切于D点.因此连接OD,OA,要证AC是⊙O的切线.因此过点O作OE⊥AC,根据等腰三角形的三线合一的性质及切线的性质,得出AO是∠BAC的平分线及OD⊥AB,根据角平分线上的点到角两边的距离相等,得出OE=OD,即可得出结论。
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的三个顶点A、B、D分别在长方形 EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为![]() ,
,![]() ,则正方形ABCD的面积为______.
,则正方形ABCD的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离![]() (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴的负半轴上,点
轴的负半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,
,![]() ,
,![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以
出发以![]() 个单位/秒的速度沿
个单位/秒的速度沿![]() 向终点
向终点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发以
出发以![]() 个单位秒的速度沿
个单位秒的速度沿![]() 向终点
向终点![]() 运动,设点
运动,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,用含
,用含![]() 的关系式表示
的关系式表示![]() ,并直接写出相应的
,并直接写出相应的![]() 范围.
范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的任意一动点,点
边上的任意一动点,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,直线
对称,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 边上的高;
边上的高;
(2)当![]() 为何值时,△
为何值时,△![]() 与△
与△![]() 重叠部分的面积最大,并求出最大值;
重叠部分的面积最大,并求出最大值;
(3)连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位![]() 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位 变化(米) | +0.2 |
| -0.4 |
| +0.3 |
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com