练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．画一画
    （1）画出线段AB绕点A顺时针旋转90°后的线段（图1）
    （2）画出线段AB绕点B逆时针旋转90°后的线段（图2）
    （3）绕点B逆时针旋转90°（图3）
    （4）绕点A顺时针旋转90°（图4）

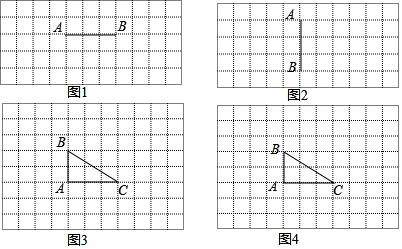
    分析 （1）根据旋转点特征，线段AB绕点A顺时针旋转90°，A点不动，B点绕点A顺时针旋转90°，得到B点的对称点，即可画出旋转后点图形；
    （2）根据旋转点特征，线段AB绕点B逆时针旋转90°，B点不动，A点绕点B逆时针旋转90°，得到A点的对称点，即可画出旋转后点图形；
    （3）分别作出所给三角形的三个顶点旋转后的对应点，再连接各对应点得到所要画的图形．
    （4）分别作出所给三角形的三个顶点旋转后的对应点，再连接各对应点得到所要画的图形．

    解答 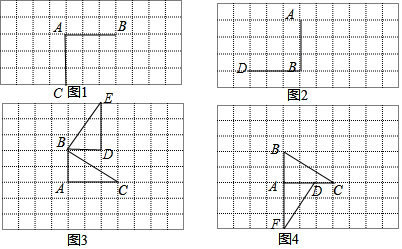解：（1）如图1所示：AC即为所求；

    （2）如图2所示：BD即为所求；

    （3）如图3所示：△BDE，即为所求；

    （4）如图4所示：△ADF，即为所求．

    点评 本题主要考查的是旋转变换的作图方法，在旋转作图时，一定要明确三个要素：旋转中心、旋转方向、旋转角度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

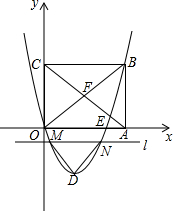    3．如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数y=x2+bx（b＜0）的图象经过点B，顶点为点D．
    （1）当t=12时，顶点D到x轴的距离等于$\frac{1}{4}$；
    （2）点E是二次函数y=x2+bx（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OE•EA的最大值及取得最大值时的二次函数表达式；
    （3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数y=x2+bx（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．龙华轻轨将于2017年6月底投入使用，拟在轨道沿途种植花木共20000棵，为尽量减少施工队交通所造成的影响，实际施工时每天的工效比原计划提高25%，结果提前5天完成种植任务，设原计划每天种植花木x棵，根据题意可列方程为（　　）
    A．$\frac{2000}{x}$-$\frac{20000}{x（1-25%）}$=5B．$\frac{20000}{x（1+25%）}$-$\frac{20000}{x}$=5
    C．$\frac{20000}{x（1-25%）}$-$\frac{20000}{x}$=5D．$\frac{20000}{x}$-$\frac{2000}{x（1+25%）}$=5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，已知∠1=∠B，∠2=∠C，则下列结论不成立的是（　　）
    A．AD∥BCB．∠B=∠CC．∠2+∠B=180°D．AB∥CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，抛物线y=$\frac{1}{3}$x2+bx+c经过A（-2$\sqrt{3}$，0）、B（0，-2）两点，点C在y轴上，△ABC为等边三角形，点D从点A出发，沿AB方向以每秒2个单位长度的速度向终点B运动，设运动时间为t秒（t＞0），过点D作DE⊥AC于点E，以DE为边作矩形DEGF，使点F在x轴上，点G在AC或AC的延长线上．

    （1）求抛物线的解析式；
    （2）将矩形DEGF沿GF所在直线翻折，得矩形D'E'GF，当点D的对称点D'落在抛物线上时，求此时点D'的坐标；
    （3）如图2，在x轴上有一点M（2$\sqrt{3}$，0），连接BM、CM，在点D的运动过程中，设矩形DEGF与四边形ABMC重叠部分的面积为S，直接写出S与t之间的函数关系式，并写出自变量t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

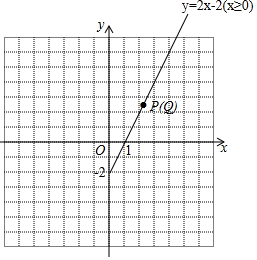    18．在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若$y'=\left\{\begin{array}{l}y（x≥0）\\-y（x＜0）\end{array}\right.$，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2）．
    结合定义，请回答下列问题：
    （1）点（-3，4）的“可控变点”为点 （-3，-4）．
    （2）若点N（m，2）是函数y=x-1图象上点M的“可控变点”，则点M的坐标为（3，2）或（-1，-2）；
    （3）点P为直线y=2x-2上的动点，当x≥0时，它的“可控变点”Q所形成的图象如图所示（实线部分含实心点）．请补全当x＜0时，点P的“可控变点”Q所形成的图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．有这样一个问题：探究函数y=|x-1|+1的图象与性质．小东根据学习一次函数的经验，对函数y=|x-1|+1的图象与性质进行了探究．
    下面是小东的探究过程，请补充完整：
    （1）在函数y=|x-1|+1中，自变量x可以是任意实数；
    如表是y与x的几组对应值．
    x…-4-3-2-101234…
    y…65432123m…
    ①求m的值；
    ②在平面直角坐标系xOy中，描出上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
    （2）结合函数图象，写出该函数的一条性质：x＜1时y随x的增大而减小，x＞1时y随x的增大而增大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列各题中，适合用平方差公式计算的是（　　）
    A．（3a+b）（3b-a）B．（$\frac{1}{3}a$+1）（-$\frac{1}{3}a$-1）C．（a-b）（-a+b）D．（-a-b）（-a+b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．投掷硬币m次，正面向上n次，其频率p=$\frac{n}{m}$，则下列说法正确的是（　　）
    A．p一定等于$\frac{1}{2}$B．p一定不等于$\frac{1}{2}$
    C．多投一次，p更接近$\frac{1}{2}$D．投掷次数逐步增加，p稳定在$\frac{1}{2}$附近

    查看答案和解析>>

    同步练习册答案