Question

1．直角梯形ABCD中，∠A=∠B=90°，E是腰AB上一点，DE⊥CD，BC=mAD，BC=nAB．

（1）如图1，若m=2，n=1，求tan∠DCE的值；
（2）如图2，若m=3，$\frac{{{S_{△DCE}}}}{{{S_{梯形ABCD}}}}=\frac{5}{16}$，求n的值；
（3）当m=2，n=$\frac{2\sqrt{3}}{3}$时，△ADE与△BCE相似．

Answer 1

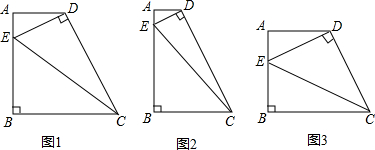
分析 （1）首先设AE=xAD，根据勾股定理，分别求出DE²、CE²、CD²的值各是多少；在Rt△CDE中，根据CE²=CD²+DE²，求出x的值各是多少；然后判断出DE=$\frac{\sqrt{5}}{2}$AD，即可求出tan∠DCE的值是多少．
（2）首先设AE=xAD，根据勾股定理，分别求出DE²、CE²、CD²的值各是多少；在Rt△CDE中，根据CE²=CD²+DE²，求出x、n的关系；然后根据$\frac{{{S_{△DCE}}}}{{{S_{梯形ABCD}}}}=\frac{5}{16}$，求出n的值是多少即可．
（3）首先根据△ADE与△BCE，BC=2AD，判断出BE=2AE，CE=2DE；然后根据勾股定理，分别求出DE²、CD²的值各是多少，再根据CE=2DE，CE²=CD²+DE²，判断出CD²=3DE²，即可求出n的值是多少．

解答 解：（1）如图1，作DF⊥BC于点F，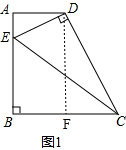

∵BC=2AD，BC=AB，
∴AB=2AD，
设AE=xAD，
则BE=（2-x）AD，
在Rt△ADE中，
DE²=AD²+AE²=（1+x²）AD²，
在Rt△BCE中，
CE²=BC²+BE²=4AD²+（2-x）²AD²=（x²-4x+8）AD²，
在Rt△CDF中，
CD²=CF²+DF²=（2AD-AD）²+（2AD）²=5AD²，
在Rt△CDE中，
∵CE²=CD²+DE²，
∴（x²-4x+8）AD²=5AD²+（1+x²）AD²=（x²+6）AD²，
解得x=0.5，
∴DE²=（1+0.25）AD²=1.25AD²，
∴DE=$\frac{\sqrt{5}}{2}$AD，
∴tan∠DCE=$\frac{DE}{CD}$=$\frac{\frac{\sqrt{5}}{2}AD}{\sqrt{5}AD}=\frac{1}{2}$．

（2）如图2，作DF⊥BC于点F，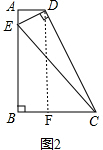

∵BC=3AD，BC=nAB，
∴AB=$\frac{3}{n}$AD，
设AE=xAD，
则BE=（$\frac{3}{n}$-x）AD，
在Rt△ADE中，
DE²=AD²+AE²=（1+x²）AD²，
在Rt△BCE中，
CE²=BC²+BE²=9AD²+（$\frac{3}{n}$-x）²AD²=（x²-$\frac{6}{n}$x+$\frac{9}{{n}^{2}}$+9）AD²，
在Rt△CDF中，
CD²=CF²+DF²=（3AD-AD）²+$\frac{9}{{n}^{2}}$AD²=（$\frac{9}{{n}^{2}}$+4）AD²，
在Rt△CDE中，
∵CE²=CD²+DE²，
∴（x²-$\frac{6}{n}$x+$\frac{9}{{n}^{2}}$+9）AD²=（$\frac{9}{{n}^{2}}$+4）AD²+（1+x²）AD²=（x²+$\frac{9}{{n}^{2}}$+5）AD²，
解得x=$\frac{2}{3}$n．
∵${{（S}_{△DCE}）}^{2}$=${（\frac{1}{2}CD•DE）}^{2}$=$\frac{1}{4}$（$\frac{9}{{n}^{2}}$+4）AD²•（1+x²）AD²=$\frac{1}{4}$（$\frac{9}{{n}^{2}}$+4）（1+$\frac{4}{9}$n²）AD⁴，
∴S_△DCE=$\frac{{4n}^{2}+9}{6n}$AD²，
又∵S_梯形ABCD=$\frac{1}{2}$（AD+BC）AB=$\frac{1}{2}$（AD+3AD）•$\frac{3}{n}$AD=$\frac{6}{n}$AD²，
∴$\frac{{S}_{△DCE}}{{S}_{梯形ABCD}}$=$\frac{{\frac{{4n}^{2}+9}{6n}AD}^{2}}{{\frac{6}{n}AD}^{2}}$=$\frac{{4n}^{2}+9}{36}$=$\frac{5}{16}$，
解得n=$\frac{3}{4}$或n=-$\frac{3}{4}$（舍去）．

（3）如图3，作DF⊥BC于点F，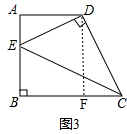

∵BC=2AD，BC=nAB，
∴$\frac{BC}{AD}=2$，AB=$\frac{2}{n}$AD，
∵△ADE与△BCE，
∴$\frac{BE}{AE}=\frac{CE}{DE}=\frac{BC}{AD}$=2，
∴BE=2AE，CE=2DE，
∴AE=$\frac{1}{3}$AB=$\frac{2}{3n}$AD，BE=$\frac{4}{3n}$AD，
在Rt△ADE中，
DE²=AD²+AE²=（1+$\frac{4}{{9n}^{2}}$）AD²，
在Rt△CDF中，
CD²=CF²+DF²=（2AD-AD）²+$\frac{4}{{n}^{2}}$AD²=（$\frac{4}{{n}^{2}}$+1）AD²，
∵CE=2DE，
∴CE²=4DE²，
又∵CE²=CD²+DE²，
∴CD²=3DE²，
∴（$\frac{4}{{n}^{2}}$+1）AD²=（1+$\frac{4}{{9n}^{2}}$）AD²×3，
解得n=$\frac{2\sqrt{3}}{3}$或n=-$\frac{2\sqrt{3}}{3}$（舍去），
∴当m=2，n=$\frac{2\sqrt{3}}{3}$时，△ADE与△BCE相似．
故答案为：$\frac{2\sqrt{3}}{3}$．

点评 （1）此题主要考查了相似形综合题，考查了分析推理能力，考查了数形结合思想的应用，要熟练掌握．
（2）此题还考查了三角形相似的判定和性质的应用，要熟练掌握，解答此题的关键是要明确：①三边法：三组对应边的比相等的两个三角形相似；②两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；③两角法：有两组角对应相等的两个三角形相似．
（3）此题还考查了勾股定理的应用，要熟练掌握．