Question

17．如图1，直线l：y=-$\frac{3}{4}$x+3分别交x轴，y轴于B，A两点，等腰Rt△CDE的斜边CD在x轴上，且CD=6．若直线l以每秒3个单位的速度向上匀速运动，同时点C从（6，0），开始以每秒2个单位的速度向右匀速运动（如图2），设运动后直线l分别交x轴，y轴于N，M两点，以OM，ON为边作如图所示的矩形OMPN，设运动时间为t秒．
（1）运动t秒后点E坐标为（9+2t，3），点N坐标为（4+4t，0）（用含t的代数式表示）；
（2）设矩形OMPN与运动后的△CDE的重叠部分面积为S，求S与t的函数关系式，并写出相应的t的取值范围；
（3）若直线l和△CDE运动后，直线l上存在点Q使∠OQC=90°，则当在线段MN上符合条件的点Q有且只有两个时，求t的取值范围；
（4）连接PC，PE，当△PCE是等腰三角形时，直接写出t的值．

Answer 1

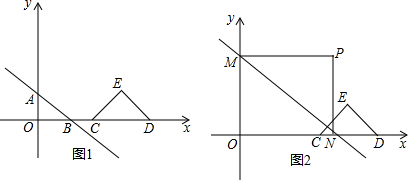
分析 （1）过E作EG⊥CD于G，根据等腰直角三角形的性质求出CG=DG=EG=3，求出B的坐标，即可得到E、N的坐标；
（2）①0＜t＜1时，s=0②1＜t≤2.5，如图2，S=$\frac{1}{2}$CG•GH，把CG、GH代入即可求出答案；③当2.5＜t＜4时，如图（3）同法可求DP，根据s=S_△CHD-S_△DQG，求出△CHD和△DQG的面积代入即可；④当t≥4时，s=S_△CHD=$\frac{1}{2}$×6×3=9；
（3）①直线L经过点C，即C、Q重合，根据4+4t=6+2t，求出即可；②如图直线L切圆于F，证△QFE∽△QOW，得出$\frac{EQ}{QW}$=$\frac{EF}{OW}$，代入即可求出t的值，进一步得出t的取值范围；
（4）分PC=PE，PC=CE及CE=PE时三种情况进行讨论．

解答 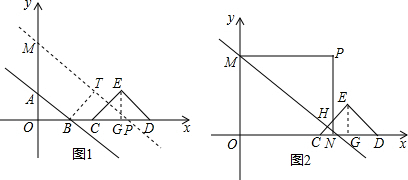解；（1）过E作MG⊥CD于G，
∵等腰直角△CDE，
∴CG=DG=MG=3，
由勾股定理得：EC=ED=3$\sqrt{2}$，
∵点C从（6，0）开始以每秒2个单位的速度向右作匀速平移运动，
∴OG=6+3+2t=9+2t，
∵y=-$\frac{3}{4}$x+3，
∴当y=0时，x=4，
∴B（4，0），
∵直线l以每秒3个单位向上作匀速平移运动，
∴直线PM的解析式是y=-$\frac{3}{4}$x+3+3t，
y=0代入得：0=-$\frac{3}{4}$x+3+3t，
x=4t+4
∴OP=4+4t，
∴E（9+2t，3），N（4+4t，0），
故答案为：（9+2t，3），（4+4t，0）．

（2）①∵当两图形不重合时，
∵B（4，0），
∴OB=4，此时BC=2，点B运动速度为4个单位每秒，点C运动速度为2个单位每秒，若点B经过t秒追上点C，则4t-2t=2，故t=1秒，所以t的范围是：0＜t＜1，s=0，如图1，
②∵当t=2.5时，PN过E点，
∴1＜t≤2.5，如图2，由矩形OMPN，∠ONH=90°，
∵∠ECD=45°=∠CHN，
∴CN=（4+4t）-（6+2t）=2t-2=NH，
∴S=$\frac{1}{2}$CN•NH=$\frac{1}{2}$（2t-2）²=2t²-4t+2，
即：s=2t²-4t+2；
③∵当t=4时，PN过D点，
∴当2.5＜t＜4时，如图3：
同法可求DN=OD-ON=（6+6+2t）-（4+4t）=8-2t，
∴s=S_△CED-S_△DNH=$\frac{1}{2}$×6×3-$\frac{1}{2}$（8-2t）²=-2t²+16t-23，
即：s=-2t²+16t-23；

④∵当t≥4时，如图4，△EDC在矩形OMPN的内部，
∴当t≥4时，s=S_△CMD=$\frac{1}{2}$×6×3=9；
答：S与t的函数关系式是s=2t²-4t+2（1＜t≤2.5）或s=-2t²+16t-23（2.5＜t＜4）或s=9（t≥4）．

（3）解：①如图5，直线L经过点C，即C、N重合，
此时4+4t=6+2t，
解得：t=1；
②如图6，直线L切圆于F，即点T，OE=EF=3+t，EN=1+3t
∵∠FNC=∠FNC，∠EFN=∠COW=90°，
∴△NFE∽△NOW，
∴$\frac{EN}{NW}$=$\frac{EF}{OW}$，
$\frac{1+3t}{\sqrt{（-\frac{9}{4}t+3）^{2}+（3+t+1+3t）^{2}}}$=$\frac{3+t}{-\frac{9}{4}t+3}$，解得：t=3，
∴1＜t＜3，
答：t的取值范围是1＜t＜3．

（4）∵A（0，3），B（4，0），
∴M（0，3+3t），N（4+4t，0）．
∵四边形OMPN是矩形，
∴P（4+4t，3+3t）．
∵C（6+2t，0），E（9+2t，3），
∴当PC=PE时，（6+2t-4-4t）²+（-3-3t）²=（9+2t-4-4t）²+（3-3-3t）²，解得t=0.4（秒）；
当PC=CE时，（6+2t-4-4t）²+（-3-3t）²=（9+2t-6-2t）²+3²，解得t₁=$\frac{-5+3\sqrt{10}}{13}$，t₂=$\frac{-5-3\sqrt{10}}{13}$（舍去）；
当CE=PE时，（9+2t-6-2t）²+3²=（9+2t-4-4t）²+（3-3-3t）²，解得t₁=1，t₁=$\frac{7}{13}$．
综上所述，当t=0.4秒或$\frac{-5+3\sqrt{10}}{13}$秒或1秒或$\frac{7}{13}$秒时，△PCE是等腰三角形．

点评 本题考查的是一次函数综合题，涉及到等腰直角三角形的性质、矩形的性质、切线的判定与性质等知识，在解答（4）时要注意进行分类讨论．