
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
【答案】(1)普通列车的行驶路程是520千米;(2)高铁的平均速度是300千米/时
【解析】
(1)设高铁的行驶路程为x千米,则普通列车的行驶路程为1.3x千米,根据“普通列车的行驶路程+高铁的行驶路程=920千米”列出方程并解答.
(2)设普通列车平均速度是a千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可.
解:(1)设高铁的行驶路程为x千米,则普通列车的行驶路程为1.3x千米,
依题意得:x+1.3x=920
解得x=400.
所以1.3x=520(千米)
答:普通列车的行驶路程是520千米;
(2)设普通列车平均速度是a千米/时,则高铁平均速度是2.5a千米/时,根据题意得:
![]()
解得:a=120,
经检验a=120是原方程的解,
则高铁的平均速度是120×2.5=300(千米/时),
答:高铁的平均速度是300千米/时


科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
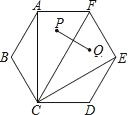
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
销售单价x(元) | 50 | 60 | 70 | 80 |
销售数量y(万件) | 5.5 | 5 | 4.5 | 4 |
(1)求y与x的函数关系式;
(2)问:当销售单价x为何值时,该公司年利润最大?并求出这个最大值;
【备注:年利润=年销售额﹣总进货价﹣其他开支】
(3)若公司希望年利润不低于60万元,请你帮助该公司确定销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
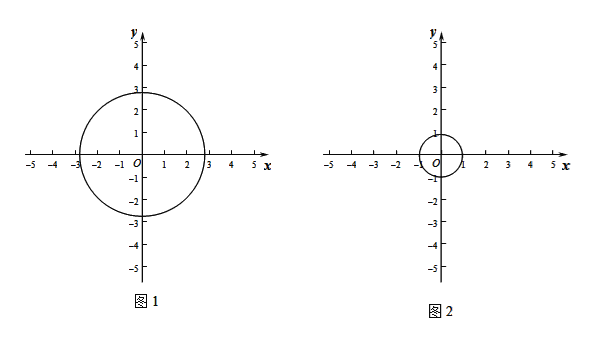
【题目】在平面直角坐标系中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2![]() ,
,
①判断M(2,0),N(﹣2,1)两个点的变换点M′、N′与⊙O的位置关系;
②若点P在直线y=x-2上,点P的变换点P′不在⊙O外,结合图形求点P横坐标x的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+5上,求点P与⊙O上任意一点距离的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
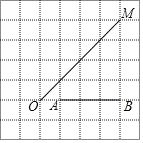
【题目】如图,在每个小正方形的边长为1的网格中,点O,A,B,M均在格点上,P为线段OM上的一个动点.
(1)OM的长等于_______;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com