
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

【答案】(1)![]() , D (
, D (![]() ,
,![]() );(2)△ABC是直角三角形,证明见解析;
);(2)△ABC是直角三角形,证明见解析;
(3)M(![]() ,0).
,0).
【解析】(1)∵点A(-1,0)在抛物线y=![]() x2 + bx-2上,
x2 + bx-2上,
∴![]() × (-1 )2 + b× (-1)–2 = 0,
× (-1 )2 + b× (-1)–2 = 0,
![]() 解得b =
解得b =![]() ,
,
∴ 抛物线的解析式为y=![]() x2-
x2-![]() x-2.
x-2.
y= ( x2 -3x- 4 ) =![]() (x-)2-
(x-)2-![]() ,
,
∴顶点D的坐标为 (![]() , -
, -![]() ).
).
(2)当x = 0时y = -2,
∴C(0,-2),OC = 2。
当y = 0时, ![]() x2-
x2-![]() x-2 = 0,
x-2 = 0,
∴x1 =-1, x2 = 4,
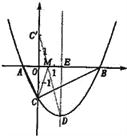
∴B (4,0)
∴OA = 1, OB = 4, AB = 5.
∵AB2 = 25, AC2 = OA2 + OC2 = 5, BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2.
∴△ABC是直角三角形.
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2,连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC + MD的值最小及△DCM的周长最小
设抛物线的对称轴交x轴于点E.
∵ED∥y轴, ∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴![]()
∴![]() , ∴m =
, ∴m =![]() .
.
所以M的坐标为(![]() ,0)
,0)


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD的边AD=2AB,点E、A、B、F在一条直线上,且AE=BF=AB,EC交AD于M,FD交BC于N.

(1) △AEM≌△DCM吗?说明理由.
(2) 四边形CDMN是菱形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对![]() ,
,![]() 定义一种新的运算
定义一种新的运算![]() ,规定:
,规定:![]()
 (其中
(其中![]() ).已知
).已知![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)若关于正数![]() 的不等式组
的不等式组 恰好有2个整数解,求
恰好有2个整数解,求![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 时,满足条件的
时,满足条件的![]() ,
,![]() 的关系.
的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(-2,0)和(-1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=-2x上时,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是弧BC的中点,过点D作DE⊥AC,交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连结BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com