
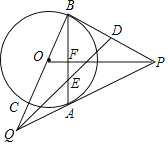
【题目】如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.
(1)求证:AC∥PO;
(2)设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】(1)根据切线长定理得出PA=PB,且PO平分∠BPA,利用等腰三角形三线合一的性质得出PO⊥AB.根据圆周角定理得出AC⊥AB,进而得到AC∥PO;
(2)连结OA、DF.先用勾股定理计算出AQ=4,再计算出PA=PB=6,利用切线长定理可得到F点为AB的中点,易得DF为△BAP的中位线,则DF=![]() PA=3,DF∥PA,利用DF∥AQ得到△DFE∽△QEA,所以
PA=3,DF∥PA,利用DF∥AQ得到△DFE∽△QEA,所以![]() ,设AE=4t,FE=3t,则AF=AE+FE=7t,于是BE=BF+FE=AF+FE=7t+3t=10t,最后计算
,设AE=4t,FE=3t,则AF=AE+FE=7t,于是BE=BF+FE=AF+FE=7t+3t=10t,最后计算![]() .
.
(1)证明:∵PA、PB是⊙O的两条切线,A、B是切点,
∴PA=PB,且PO平分∠BPA,
∴PO⊥AB.
∵BC是直径,
∴∠CAB=90°,
∴AC⊥AB,
∴AC∥PO;
(2)连结OA、DF,如图,

∵PA、PB是⊙O的两条切线,A、B是切点,
∴∠OAQ=∠PBQ=90°.
在Rt△OAQ中,OA=OC=3,
∴OQ=5.
由QA2+OA2=OQ2,得QA=4.
在Rt△PBQ中,PA=PB,QB=OQ+OB=8,由QB2+PB2=PQ2,得82+PB2=(PB+4)2,解得PB=6,
∴PA=PB=6.
∵OP⊥AB,
∴BF=AF=![]() AB.
AB.
又∵D为PB的中点,
∴DF∥AP,DF=![]() PA=3,
PA=3,
∴△DFE∽△QEA,
∴![]()
设AE=4t,FE=3t,则AF=AE+FE=7t,
∴BE=BF+FE=AF+FE=7t+3t=10t,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
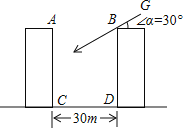
【题目】两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.
(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?
(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部.
查看答案和解析>>
科目:初中数学 来源: 题型:
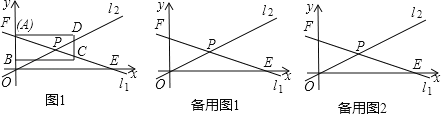
【题目】如图,在平面直角坐标系中,点F的坐标为(0,10).点E的坐标为(20,0),直线l1经过点F和点E,直线l1与直线l2 、y=![]() x相交于点P.
x相交于点P.
(1)求直线l1的表达式和点P的坐标;
(2)矩形ABCD的边AB在y轴的正半轴上,点A与点F重合,点B在线段OF上,边AD平行于x 轴,且AB=6,AD=9,将矩形ABCD沿射线FE的方向平移,边AD始终与x 轴平行.已知矩形ABCD以每秒![]() 个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
个单位的速度匀速移动(点A移动到点E时止移动),设移动时间为t秒(t>0).
①矩形ABCD在移动过程中,B、C、D三点中有且只有一个顶点落在直线l1或l2上,请直接写出此时t的值;
②若矩形ABCD在移动的过程中,直线CD交直线l1于点N,交直线l2于点M.当△PMN的面积等于18时,请直接写出此时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.
(1)当k=2时,直线l1、l2与x轴围成的三角形的面积S2=______;
(2)当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2,S3,S4,……,S2018,则S2+S3+S4+……+S2018=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
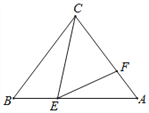
【题目】如图,在△ABC中,已知AC=BC=5,AB=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.当以点C为圆心,以CF为半径的圆与AB相切时,则BE的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com