
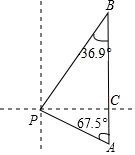
 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.分析 首先根据题意可得PC⊥AB,然后设PC=x海里,分别在Rt△APC中与Rt△PCB中,利用正切函数求得出AC与BC的长,由AB=21×5,即可得方程,解此方程求得x的值即可.
解答 解:设PC=x海里.
在Rt△APC中,∵tan∠A=$\frac{PC}{AC}$,
∴AC=$\frac{PC}{tan67.5°}$=$\frac{5x}{12}$,
在Rt△PCB中,∵tan∠B=$\frac{PC}{BC}$,
∴BC=$\frac{x}{tan36.9°}$=$\frac{4x}{3}$,
∵AC+BC=AB=21×5,
∴$\frac{5x}{12}+\frac{4x}{3}$=21×5,
解得:x=60,
即轮船行驶过程中与小岛P的最短距离PC为60海里.
点评 此题考查了方向角问题.此题难度适中,注意结合实际问题,利用解直角三角形的相关知识求解是解此题的关键,注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a2b-a2b=2 | |
| B. | 使式子$\sqrt{x+2}$有意义的x的取值范围是x>-2 | |
| C. | 单项式-x2的系数是-1 | |
| D. | 若分式$\frac{{{a^2}-1}}{a+1}$的值等于0,则a=±1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(±3)^{2}}$=±3 | B. | 23×24=27 | C. | -2a2•3a=6a3 | D. | 3m2÷(3m-1)=m-3m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
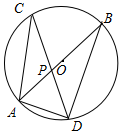 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=66°.
如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=66°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com