
���� ��1����Ϊx��-2��-2��x��4��x��4����������ɣ�
��2����x��-1��-1��x��1��x��1�ֱ��x��ȡֵ��Χȷ������ʽֵ�ķ�Χ���Ӷ��������ʽ�����ֵ��
��� �⣺��1����x��-2ʱ��|x+2|+|x-4|=-x-2+4-x=-2x+2��
��-2��x��4ʱ��|x+2|+|x-4|=x+2+4-x=6��
��x��4ʱ��|x+2|+|x-4|=x+2+x-4=2x-2��
��2����x��-1ʱ��ԭʽ=3x+5��2��
��-1��x��1ʱ��ԭʽ=-5x-3��-8��-5x-3��2��
��x��1ʱ��ԭʽ=-3x-5��-8��
��|x-1|-4|x+1|�����ֵΪ2��
���� ������Ҫ�����˾���ֵ������Ĺؼ����ܸ��ݲ���������Ϣ���ҵ����ʵķ������


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
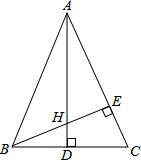 ��֪�ڡ�ABC�У���BAC����ǣ�AB=AC��AD��BE�Ǹߣ���AE=BE����֤��AH=2BD��
��֪�ڡ�ABC�У���BAC����ǣ�AB=AC��AD��BE�Ǹߣ���AE=BE����֤��AH=2BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x-��y-x��=x-y-z | B�� | -��x-y+z��=-x-y-z | ||
| C�� | x+2y-2z=x-2��y-z�� | D�� | -a+c+d+b=-��a-b��+��c+d�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������ϣ��Գ���Ϊֱ��x=-1�����㣨-1��-2�� | |
| B�� | �������ϣ��Գ���Ϊֱ��x=1�����㣨1��-2�� | |
| C�� | �������£��Գ���Ϊֱ��x=-1�����㣨1��2�� | |
| D�� | �������£��Գ���Ϊֱ��x=1�����㣨1��-2�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com