
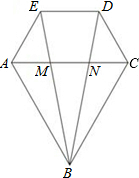
 如图是小红设计的钻石形商标,△ABC是边长为2的等边三角形,四边形ACDE是等腰梯形,AC∥ED,∠EAC=60°,AE=1.
如图是小红设计的钻石形商标,△ABC是边长为2的等边三角形,四边形ACDE是等腰梯形,AC∥ED,∠EAC=60°,AE=1.| AN |
| CN |
| AB |
| CD |
| 1 |
| 3 |
| 1 |
| 3 |
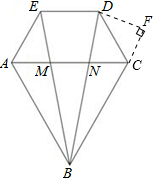 (1)证明:∵△ABC是等边三角形,
(1)证明:∵△ABC是等边三角形,| AB |
| DC |
| 2 |
| 1 |
| AN |
| CN |
| AB |
| CD |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| CD2-CF2 |
12-(
|
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| ||
| 2 |
| BF2+DF2 |
(
|
| 7 |


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:2012年四川省眉山市仁寿县文宫学区中考数学模拟试卷(四)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年湖南省郴州市临武县楚江中学中考数学模拟试卷(六)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2012年湖北省宜昌市枝江市安福寺中学中考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年湖南省益阳市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com