
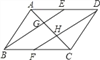
【题目】已知:如图,在ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于C、H.请判断下列结论:(1)BE=DF;(2)AG=GH=HC;(3)EG=![]() BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
BG;(4)S△ABE=3S△AGE.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】分析:(1)根据BF∥DE,BF=DE可证BEDF为平行四边形;(2)根据平行线等分线段定理判断;(3)根据△AGE∽△CGB可得;
(4)由(3)可得△ABG的面积=△AGE面积×2.
详解:(1)∵ABCD,∴AD=BC,AD∥BC.
E、F分别是边AD、BC的中点,
∴BF∥DE,BF=DE.
∴BEDF为平行四边形,BE=DF.故正确;
(2)根据平行线等分线段定理可得AG=GH=HC.故正确;
(3)∵AD∥BC,AE=![]() AD=
AD=![]() BC,
BC,
∴△AGE∽△CGB,AE:BC=EG:BG=1:2,
∴EG=![]() BG.故正确.
BG.故正确.
(4)∵BG=2EG,∴△ABG的面积=△AGE面积×2,
∴S△ABE=3S△AGE.故正确.
故选:D.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】问题背景:在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为 ![]() ),在网格中画出格点
),在网格中画出格点 ![]() (即
(即 ![]() 三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
三个顶点都在小正方形的顶点处),如图所示,这样借用网格就能计算出它的面积.
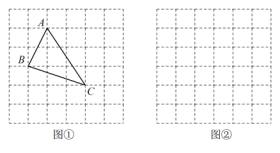
(1)请你直接写出 ![]() 的面积为 .
的面积为 .
(2)若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() 运用构图法求出这三角形的面积.
运用构图法求出这三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣2,1),B(﹣4,1),C(﹣3,2),D(﹣1,2).

(1)在图中画出四边形ABCD,并求出四边形ABCD的面积;
(2)在图中画出四边形ABCD关于x轴的对称图形A1B1C1D1,并分别写出点A、C的对应点A1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将等腰直角三角形ABC(AB=AC,∠BAC=90°)和等腰直角三角形DEF(DE=DF,∠EDF=90°)按图1摆放,点D在BC边的中点上,点A在DE上.

(1)填空:AB与EF的位置关系是 ;
(2)△DEF绕点D按顺时针方向转动至图2所示位置时,DF,DE分别交AB,AC于点P,Q,求证:∠BPD+∠DQC=180°;
(3)如图2,在△DEF绕点D按顺时针方向转动过程中,始终点P不到达A点,△ABC的面积记为S1,四边形APDQ的面积记为S2,那么S1与S2之间是否存在不变的数量关系?若存在,请写出它们之间的数量关系并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
⑴用含t的代数式表示:AP= ,AQ= .
⑵当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲跑步中途改为步行,到达图书馆恰好用30 min.小东骑自行车以300 m/min的速度直接回家.两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图9所示.
(1)家与图书馆之间的路程为 m,小玲步行的速度为 m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com