
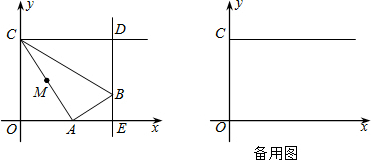
 ��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ�
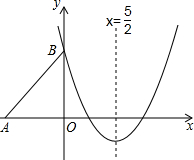
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ����ԭ�㣬A��B���������ֱ�Ϊ��-3��0������0��4����������y=$\frac{2}{3}$x2+bx+c������B���Ҷ�����ֱ��x=$\frac{5}{2}$�ϣ����� ��1����C���������y=$\frac{2}{3}$x2+bx+c�õ�c=4�����öԳ��᷽�̿����b=-$\frac{10}{3}$���Ӷ��ɵõ������߽���ʽ��
��2�������ù��ɶ��������AB=5����������ε����ʺ�ƽ�Ƶ����ʿɵ�C��5��4����D��2��0����Ȼ����ݶ��κ���ͼ���ϵ�������������жϵ�C�͵�D���������������ϣ�
��3�����������ߵĶԳ��Կɵõ�B���CΪ�������ϵĶԳƵ㣬CD���Գ��ύ�ڵ�P����������֮���߶���̿ɵõ���ʱ��P���ʹ��PBD���ܳ���С���������ô���ϵ�������ֱ��CD�Ľ���ʽΪy=$\frac{4}{3}$x-$\frac{8}{3}$��
Ȼ�����ֱ��CD��ֱ��x=$\frac{5}{2}$�Ľ������꼴�ɵõ�P�����ꣻ
��4����Գ��ύx���ڵ�F���˶�ʱ��Ϊt�룬��OM=4t��ON=t���������������ʽ�������������ʽ������S��PMN=S����OMPF-S��OMN-S��PFN�ɵ�S��PMN=-2t2+$\frac{16}{3}$t��Ȼ����ݶ��κ������������0��t��1ʱS�����ֵ��
��� �⣺��1����������y=$\frac{2}{3}$x2+bx+c����B��0��4����
��c=4��
�߶�����ֱ��x=$\frac{5}{2}$�ϣ�
��-$\frac{b}{2a}$=-$\frac{3b}{4}$=$\frac{5}{2}$�����b=-$\frac{10}{3}$��
�������߽���ʽΪy=$\frac{2}{3}$x2-$\frac{10}{3}$x+4��
��2����C�͵�D�ڸ��������ϣ��������£�
��Rt��ABO����OA=3��OB=4��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5��
���ı���ABCD�����Σ�
��BC=CD=DA=AB=5��
��C��5��4����D��2��0����
��x=5ʱ��y=$\frac{2}{3}$x2-$\frac{10}{3}$x+4=$\frac{2}{3}$��52-$\frac{10}{3}$��5+4=4��
��x=2ʱ��y=$\frac{2}{3}$x2-$\frac{10}{3}$x+4=$\frac{2}{3}$��22-$\frac{10}{3}$��2+4=0��
���C�͵�D���������������ϣ�
��3����ͼ1����BC��x�ᣬ
���B���CΪ�������ϵĶԳƵ㣬
����CD��CD���Գ��ύ�ڵ�P����PB+PD=PC+PD=CD�����ʱPB+PD��С�����ԡ�PBD���ܳ���С��
��ֱ��CD�Ľ���ʽΪy=kx+p��
��C��5��4����D��2��0�������$\left\{\begin{array}{l}{5k+p=4}\\{2k+p=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{p=-\frac{8}{3}}\end{array}\right.$��
��ֱ��CD�Ľ���ʽΪy=$\frac{4}{3}$x-$\frac{8}{3}$��
��x=$\frac{5}{2}$ʱ��y=$\frac{4}{3}$x-$\frac{8}{3}$=$\frac{4}{3}$��$\frac{5}{2}$-$\frac{8}{3}$=$\frac{2}{3}$��
��P��������$\frac{5}{2}$��$\frac{2}{3}$����
��4����Գ��ύx���ڵ�F���˶�ʱ��Ϊt�룬��OM=4t��ON=t��
S��PMN=S����OMPF-S��OMN-S��PFN
=$\frac{1}{2}$����$\frac{2}{3}$+4t����$\frac{5}{2}$-$\frac{1}{2}$��4t��t-$\frac{1}{2}$����$\frac{5}{2}$-t����$\frac{2}{3}$
=-2t2+$\frac{16}{3}$t
���κ����ĶԳ���Ϊֱ��t=-$\frac{\frac{16}{3}}{2����-2��}$=$\frac{4}{3}$��
��0��t��1��
�൱t=1ʱ��S������ֵ=-2+$\frac{16}{3}$=$\frac{10}{3}$��
���� ���⿼���˶��Ӻ������ۺ��⣺�������ն��Ӻ���ͼ���ϵ���������������κ��������ʺ����ε����ʣ�����������ͼ�����ʺ͵�ƽ�ƵĹ��ɣ������ô���ϵ������������ʽ���������·�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
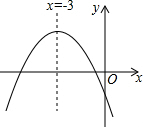 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����֪A��-1��y����B��-4��y2����C��-5��y3�����ڴ�ͼ���ϣ����й�ϵʽ��ȷ���ǣ�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����֪A��-1��y����B��-4��y2����C��-5��y3�����ڴ�ͼ���ϣ����й�ϵʽ��ȷ���ǣ�������| A�� | y1��y3��y2 | B�� | y1��y2��y3 | C�� | y3��y2=y1 | D�� | y1=y3��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com