
 如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上一点,BE=DF.
如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上一点,BE=DF.分析 (1)由四边形AEGF为矩形,ABCD为正方形,得到三个角为直角,进而确定出四边形DHGF为矩形,表示出DH,由DF与DH乘积列出y与x的关系式,并求出x的范围即可;
(2)二次函数解析式配方后,利用二次函数性质确定出四边形DHGF面积最大值,以及此时BE的值即可.
解答 解:(1)∵AEGF为矩形,ABCD为正方形,
∴∠F=∠G=∠HDF=90°,
∴四边形DHGF是矩形,
又DH=AE=AB-BE=4-x,
∴y=DF•DH=x(4-x)=-x2+4x(0<x<4);
(2)y=-x2+4x=-(x-2)2+4,
∵a=-1<0,
∴当x=2时,y有最大值为4,
则当BE为2时,四边形DHGF的面积最大,最大值是4.
点评 此题考查了二次函数的应用,熟练掌握二次函数的性质是解本题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:选择题
 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
| A. | 25.3厘米 | B. | 26.3厘米 | C. | 27.3厘米 | D. | 28.3厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
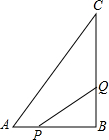 如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.
如图,△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始,沿AB边向点B以每秒1cm的速度移动;点Q从点B开始,沿着BC边向点C以每秒2cm的速度移动.如果P,Q同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
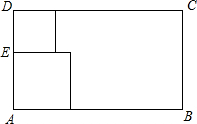 如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?
如图所示,从一张矩形纸较短的边上找一点E.过点E剪下两个正方形,它们的边长分别是AE,DE,要使剪下的两个正方形的面积和最小,点E应选在何处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
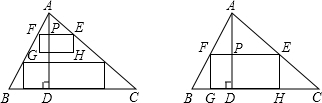 如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).
如图,△ABC中,BC=10cm,BC边上的高AD=8cm,E、F分别为AC、AB上的点,且EF∥BC,以EF为边向下作矩形EFGH,且满足EF=2FG,设EF的长为x(cm),矩形EFGH与△ABC重叠部分的面积为y(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com