
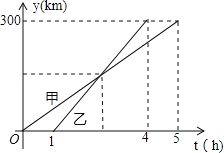
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的结论有_____.
.其中正确的结论有_____.
【答案】①②
【解析】
观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
由图象可知,A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得,k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
![]() ,
,
解得![]() ,
,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲﹣y乙|=50,可得|60t﹣100t+100|=50,即|100﹣40t|=50,
当100﹣40t=50时,可解得t=![]() ,
,
当100﹣40t=﹣50时,可解得t=![]() ,
,
又当t=![]() 时,y甲=50,此时乙还没出发,
时,y甲=50,此时乙还没出发,
当t=![]() 时,乙到达B城,y甲=250;
时,乙到达B城,y甲=250;
综上可知当t的值为![]() 或
或![]() 或
或![]() 或t=
或t=![]() 时,两车相距50千米,
时,两车相距50千米,
∴④不正确;
综上,正确的有①②,
故答案为:①②


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
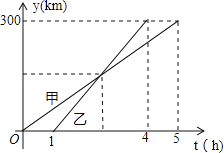
【题目】如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC= °;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=m°(m>90°)(如图2),则∠AEG﹣∠CEG= °(用m的代表式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作翻转变换,依次得到△1、△2、△3、△4…,则△23中的![]() 的坐标为_______________。
的坐标为_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
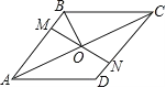
【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
A.28°B.56°C.62°D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=﹣x+m经过点A(2,0),交y轴于点B.点D为x轴上一点,且S△ADB=1.

(1)求m的值;
(2)求线段OD的长;
(3)当点E在直线AB上(点E与点B不重合),且∠BDO=∠EDA,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
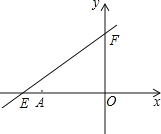
【题目】如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0)
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由;
,并说明理由;
(4)问在x轴上是否存在点Q,使得△EFQ为等腰三角形?若存在,求出符合条件的Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
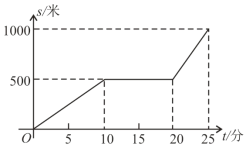
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;王老师吃早餐用了 分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com