
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.

(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
【答案】(1)证明见解析;
(2)AE的长为![]() ;
;
(3)证明见解析.
【解析】试题分析:(1)由圆的内接四边形的性质得:∠ABC+∠ADC=180°,又∠ADF+∠ADC=180°,故∠ABC=∠ADF,结合已知条件可证△ABC≌△ADF,从而可得结论;
(2)由(1)得AC=AF,由AB=AB得![]() ,得∠ADE=∠ACD.可证△ADE∽△ACD,得
,得∠ADE=∠ACD.可证△ADE∽△ACD,得![]() ,变换比例式从而得解;
,变换比例式从而得解;
(3)通过证明△ADG∽△AFD得∠ADG=∠F.再运用切线的判定定理即可得证.
试题解析:(1)证明:∵四边形ABCD内接于⊙O,∴∠ABC+∠ADC=180°.
∵∠ADF+∠ADC=180°,∴∠ABC=∠ADF.
在△ABC与△ADF中,
 ,
,
∴△ABC≌△ADF.
∴AC=AF;
(2)由(1)得,AC=AF=![]() .
.
∵AB=AD,
∴![]()
∴∠ADE=∠ACD.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴![]() .
.
∴ .
.
(3)证明:∵EG∥CF,∴ ![]() .
.
∴AG=AE.
由(2)得![]() ,∴
,∴![]() .
.
∵∠DAG=∠FAD,∴△ADG∽△AFD.
∴∠ADG=∠F.
∵AC=AF,∴∠ACD=∠F.
又∵∠ACD=∠ABD,
∴∠ADG=∠ABD.
∵BD为⊙O的直径,
∴∠BAD=90°.
∴∠ABD+∠BDA=90°.∴∠ADG+∠BDA=90°.
∴GD⊥BD.
∴DG为⊙O的切线.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
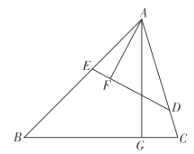
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证ΔADE∽ΔABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
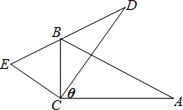
【题目】如图,△ABC中,∠ACB=90°,∠A=25°,若以点C为旋转中心,将△ABC旋转θ度到△DEC的位置,使点B恰好落在边DE上,则θ等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当a>0,b>0时:
∵(![]() )2=a﹣2
)2=a﹣2![]() +b≥0
+b≥0
∴a+b≥2![]() ,当且仅当a=b时取等号.
,当且仅当a=b时取等号.
请利用上述结论解决以下问题:
(1)请直接写出答案:当x>0时,x+![]() 的最小值为 .当x<0时,x+
的最小值为 .当x<0时,x+![]() 的最大值为 ;
的最大值为 ;
(2)若y=![]() ,(x>﹣1),求y的最小值;
,(x>﹣1),求y的最小值;
(3)如图,四边形ABCD的对角线AC、BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E,BC=3,CD=3![]()
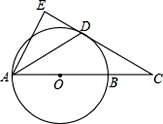
(1)求证:直线CE是⊙O的切线;
(2)求⊙O的半径;
(3)求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
科目:初中数学 来源: 题型:
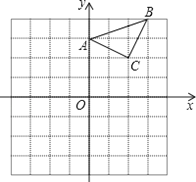
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是1个单位长度).
(1)画出△ABC关于x轴的轴对称图形,得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com