
 ≈1.414,
≈1.414, ≈1.732,结果保留两个有效数字)
≈1.732,结果保留两个有效数字)
科目:初中数学 来源: 题型:
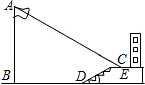 梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:
梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
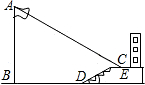 梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据:
梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.(可能用到的数据: ≈1.414,
≈1.414, ≈1.732,结果保留两个有效数字)
≈1.732,结果保留两个有效数字)查看答案和解析>>
科目:初中数学 来源:2011年3月中考数学第一次模拟考试卷(解析版) 题型:解答题
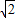 ≈1.414,
≈1.414, ≈1.732,结果保留两个有效数字)
≈1.732,结果保留两个有效数字)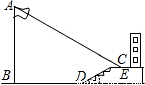
查看答案和解析>>
科目:初中数学 来源:2006年广东省梅州市中考数学试卷(解析版) 题型:解答题
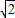 ≈1.414,
≈1.414,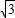 ≈1.732,结果保留两个有效数字)
≈1.732,结果保留两个有效数字)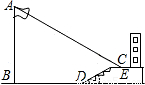
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com