
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣4,0),B(﹣1,0)两点.
(1)求抛物线的解析式;
(2)在第三象限的抛物线上有一动点D.
①如图(1),若四边形ODAE是以OA为对角线的平行四边形,当平行四边形ODAE的面积为6时,请判断平行四边形ODAE是否为菱形?说明理由.
②如图(2),直线y=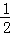 x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为
x+3与抛物线交于点Q、C两点,过点D作直线DF⊥x轴于点H,交QC于点F.请问是否存在这样的点D,使点D到直线CQ的距离与点C到直线DF的距离之比为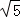 :2?若存在,请求出点D的坐标;若不存在,请说明理由.
:2?若存在,请求出点D的坐标;若不存在,请说明理由.



解:(1)把点A(﹣4,0)、B(﹣1,0)代入解析式y=ax2+bx+3,
得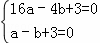 ,解得
,解得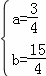 ,
,
∴抛物线的解析式为:y=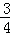 x2+
x2+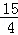 x+3.
x+3.
(2)①如答图2﹣1,过点D作DH⊥x轴于点H.
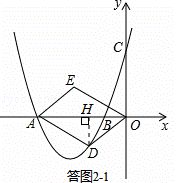
∵S▱ODAE=6,OA=4,
∴S△AOD=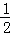 OA•DH=3,
OA•DH=3,
∴DH=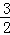 .
.
因为D在第三象限,所以D的纵坐标为负,且D在抛物线上,
∴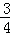 x2+
x2+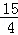 x+3=﹣
x+3=﹣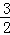 ,
,
解得:x1=﹣2,x2=﹣3.
∴点D坐标为(﹣2,﹣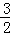 )或(﹣3,﹣
)或(﹣3,﹣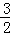 ).
).
当点D为(﹣2,﹣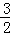 )时,DH垂直平分OA,平行四边形ODAE为菱形;
)时,DH垂直平分OA,平行四边形ODAE为菱形;
当点D为(﹣3,﹣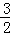 )时,OD≠AD,平行四边形ODAE不为菱形.
)时,OD≠AD,平行四边形ODAE不为菱形.
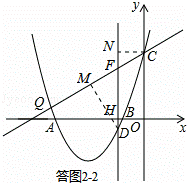
②假设存在.
如答图2﹣2,过点D作DM⊥CQ于M,过点C作CN⊥DF于N,则DM:CN=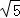 :2.
:2.
设D(m,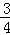 m2+
m2+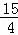 m+3)(m<0),则F(m,
m+3)(m<0),则F(m,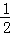 m+3).
m+3).
∴CN=﹣m,NF=﹣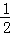 m
m
∴CF=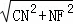 =﹣
=﹣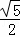 m.
m.
∵∠DMF=∠CNF=90°,∠DFM=∠CFN,
∴△DMF∽△CNF,
∴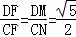 ,
,
∴DF=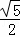 CF=﹣
CF=﹣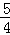 m.
m.
∴DN=NF+DF=﹣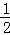 m﹣
m﹣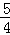 m=﹣
m=﹣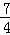 m.
m.
又DN=3﹣(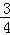 m2+
m2+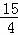 m+3)=﹣
m+3)=﹣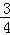 m2﹣
m2﹣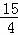 m,
m,
∴﹣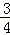 m2﹣
m2﹣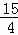 m=﹣
m=﹣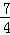 m
m
解得:m=﹣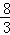 或m=0(舍去)
或m=0(舍去)
∴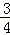 m2+
m2+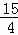 m+3=﹣
m+3=﹣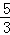
∴D(﹣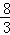 ,﹣
,﹣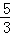 ).
).

 综上所述,存在满足条件的点D,点D的坐标为(﹣
综上所述,存在满足条件的点D,点D的坐标为(﹣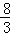 ,﹣
,﹣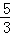 ).
).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
在2014年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数、方差依次是( )
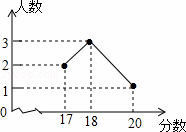
A. 18,18,1 B. 18,17.5,3 C. 18,18,3 D. 18,17.5,1


查看答案和解析>>
科目:初中数学 来源: 题型:
海南五月瓜果飘香,某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元.李叔叔购买这两种水果共30千克,共花了708元.请问李叔叔购买这两种水果各多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
大课间活动时,有两个同学做了一个数字游戏:有三张正面写有数字﹣1,0,1的卡片,它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回并洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q值,两次结果记为(p,q).
(1)请你帮他们用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数解的概率.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com