
 x2-mx+
x2-mx+ m2(m≠0)的对称轴交x轴于点P,交反比例函数y=
m2(m≠0)的对称轴交x轴于点P,交反比例函数y=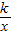 (k>0)图象于点Q,连接OQ.
(k>0)图象于点Q,连接OQ. k=2时,求证:△OPQ为等腰直角三角形;
k=2时,求证:△OPQ为等腰直角三角形;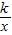 (k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.
(k>0)图象交正方形OABC的边BC、BA于M、N两点,连接AQ、BQ,有S△ABQ=4S△APQ.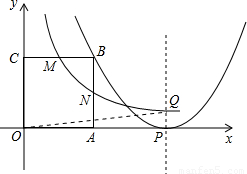
 k=2得出k的值,进而得出P,Q点坐标,即可得出△OPQ是等腰直角三角形;
k=2得出k的值,进而得出P,Q点坐标,即可得出△OPQ是等腰直角三角形; AB•AP=4×
AB•AP=4× AP•PQ,即AB=4PQ,进而得出点Q的纵坐标为
AP•PQ,即AB=4PQ,进而得出点Q的纵坐标为 或-
或- (负值舍去),再求出m的值,将B点代入即可;
(负值舍去),再求出m的值,将B点代入即可; 解:(1)∵y=
解:(1)∵y= x2-mx+
x2-mx+ m2=
m2= (x2-2mx)+
(x2-2mx)+ m2=
m2= (x-m)2,
(x-m)2, k=2,
k=2, x2-2x+2;
x2-2x+2;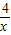 ,
,
 AB•AP=4×
AB•AP=4× AP•PQ,即AB=4PQ,
AP•PQ,即AB=4PQ,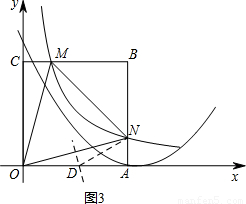
 AB=
AB= ×2=
×2= ,
, 或-
或- (负值舍去),
(负值舍去), x2-mx+
x2-mx+ m2
m2 x2-4x+8.
x2-4x+8. x2-4x+8,成立.
x2-4x+8,成立.
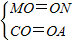 ,
,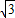 t.
t.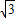 t=2,
t=2,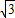 ,
,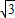 ),
),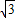 )=8-4
)=8-4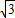 ,
,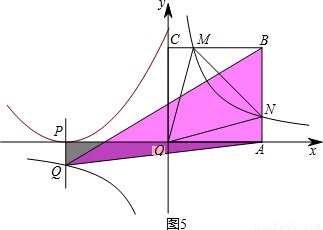
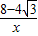 ,
, 或-
或- .
. 时,如图4,
时,如图4,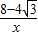 =
= ,
,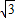 ,
,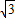 ,
,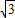 +2(8-4
+2(8-4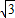 )=32-16
)=32-16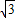 ,
, 时,如图5,
时,如图5,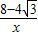 =-
=- ,
, ,
, ,
,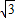 +2(8-4
+2(8-4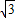 )=0.
)=0.

科目:初中数学 来源: 题型:
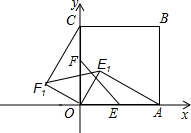 2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.
2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.查看答案和解析>>
科目:初中数学 来源: 题型:
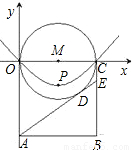
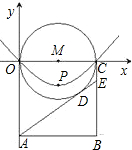 立平面直角坐标系,使点B落在第四象限,一条抛物线y=ax2+bx经过O、C两点,并将抛物线的顶点记作P.
立平面直角坐标系,使点B落在第四象限,一条抛物线y=ax2+bx经过O、C两点,并将抛物线的顶点记作P.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=-
如图,已知正方形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,抛物线y=-| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学原创试卷大赛(7)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《图形的旋转》(04)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com