
【题目】如图,直线y=kx+5经过点B(3,9)和A(﹣6,m).
(1)求k,m的值;
(2)求△AOB的面积.

【答案】(1)k的值为![]() ,m的值为﹣3;(2)
,m的值为﹣3;(2)![]() .
.
【解析】
(1)把点B(3,9)代入y=kx+5,得到关于k的一元一次方程,解之即可得到k的值,即可得到直线AB的解析式,把A(﹣6,m)代入直线AB的解析式,得到关于m的一元一次方程,解之即可得到m的值,
(2)设直线AB与x轴交于点C,△AOB被x轴分成△AOC和△BOC,分别计算△AOC和△BOC的面积,即可得到答案.
解:(1)把点B(3,9)代入y=kx+5得:
3k+5=9,
解得:![]()
即直线的解析式为:![]()
把点A(﹣6,m)代入![]() 得:
得:
![]()
即k的值为![]() ,m的值为﹣3;
,m的值为﹣3;
(2)设直线AB与x轴交于点C,如下图所示:
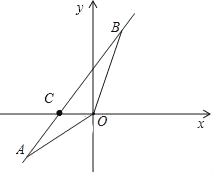
把y=0代![]() 得:
得:
![]() ,
,
![]()
即点![]()
![]()
![]()
![]()
即△AOB的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
的一个交点为P(2,m),与x轴、y轴分别交于点A,B.
(1)求m的值
(2)若PA=2AB,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,x,y满足:![]() (x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
(x-5)2+|m-2|=0,-3a2·by+1与a2b3是同类项,求整式(2x2-3xy+6y2)-m(3x2-xy+9y2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)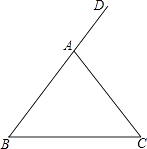
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明: 判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.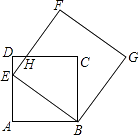
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= ![]() 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在以O为原点的平面直角坐标系中,点A的坐标为(0,2),点P(s,t)在抛物线y= ![]() x2+1上,点P到x轴的距离记为m,PA=n.
x2+1上,点P到x轴的距离记为m,PA=n.
(1)若s=4,分别求出m、n的值,并比较m与n的大小关系;
(2)若点P是该抛物线上的一个动点,则(1)中m与n的大小关系是否仍成立?请说明理由;
(3)如图2,过点P的直线y=kx(k≠0)与抛物线交于另一点Q连接PA、QA,是否存在k使得PA=2QA?若存在,请求出k的值;若不存在,请举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.
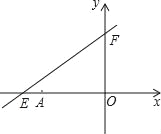
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA= ![]() ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求 ![]() 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com