
 如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为$\frac{75}{8}$.
如图,矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为$\frac{75}{8}$. 分析 根据矩形的性质和勾股定理求出BD,证明△BOF∽△BCD,根据相似三角形的性质得到比例式,求出BF,根据勾股定理求出OF,根据三角形的面积公式计算即可.
解答 解:∵四边形ABCD是矩形,
∴∠A=90°,又AB=6,AD=BC=8,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10,
∵EF是BD的垂直平分线,
∴OB=OD=5,∠BOF=90°,又∠C=90°,
∴△BOF∽△BCD,
∴$\frac{BO}{BC}$=$\frac{BF}{BD}$,即$\frac{5}{8}$=$\frac{BF}{10}$,
解得,BF=$\frac{25}{4}$,
则OF=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\frac{15}{4}$,
则△BOF的面积=$\frac{1}{2}$×OF×OB=$\frac{75}{8}$,
故答案为:$\frac{75}{8}$.
点评 本题考查的是矩形的性质、线段垂直平分线的性质以及勾股定理的应用,掌握矩形的四个角是直角、对边相等以及线段垂直平分线的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
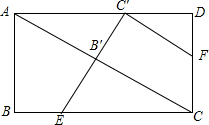 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 审查书稿中有哪些学科性错误适合用抽样调查法 | |
| C. | 甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )| A. | 175πcm2 | B. | 350πcm2 | C. | $\frac{800}{3}$πcm2 | D. | 150πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18.1×105 | B. | 1.81×106 | C. | 1.81×107 | D. | 181×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=78}\\{3x+2y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=78}\\{2x+3y=30}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=30}\\{2x+3y=78}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{3x+2y=78}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com