正方形ABCD的对角线交点为O,两条对角线把它分成了四个面积相等的三角形.
(1)平行四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(2)四边形ABCD的两条对角线互相垂直,交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(3)四边形ABCD的两条对角线交点为O,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试判断S1,S2,S3,S4的关系,并加以证明;
(4)四边形ABCD的两条对角线相等,交点为O,∠BAC=∠BDC,若△AOB,△BOC,△COD,△DOA面积分别为S1,S2,S3,S4,试只用S1,S3或只用S2,S4表示四边形ABCD的面积S.
分析:(1)根据平行四边形的性质可证得四个小三角形面积相等;
(2)我们可以表示出这四个面积,S
1=
OA•OB,S
2=
OB•OC,S
3=
OC•OD,S
4=
OD•OA,于是我们发现S
1S
3=S
2S
4;
(3)虽然两条对角线不垂直了,但是思路和(2)是一样的;
(4)应该分AB与CD平行或不平行两种情况进行分析.
解答: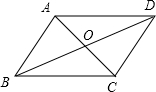
解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,
∵△AOB,△BOC的边OA,OC上的高相同,
∴S
1=S
2,
同理S
2=S
3,S
3=S
4,S
4=S
1,
∴S
1=S
2=S
3=S
4.
(2)∵AC⊥BD,垂足为O,
∴S
1=
OA•OB,S
2=
OB•OC,S
3=
OC•OD,S
4=
OD•OA,
∴S
1S
3=S
2S
4;
(3)设点B到线段AC所在直线的距离为h
1,点D到线段AC所在直线的距离为h
2,
∴S
1=
OA•h
1,S
2=
OC•h
1,S
3=
OC•h
2,S
4=
OA•h
2,
∴S
1S
3=S
2S
4;
(4)∵BAC=∠BDC,∠AOB=∠DOC,
∴∠DCA=∠ABD,
当AB与CD不平行时,必相交于一点,
设线段BA与CD的延长线交于点E,
∵AC=BD,∠AEC=∠DEB,
∴△AEC≌△DEB,
∴AE=DE,CE=BE,
∴AB=DC,
∴△AOB≌△DOC,
∴S
1=S
3,
∵S
1S
3=S
2S
4,
∴S
12=S
2S
4,
∴S=S
1+S
2+S
3+S
4=2S
1+S
2+S
4=S
2+S
4+2
(或=(
+
)
2);
当AB与CD平行时,则△ABD与△BAC同底等高,有S
1+S
2=S
1+S
4,
∴S
2=S
4,
∵S
1S
3=S
2S
4,
∴S
22=S
1S
3,S=S
1+S
3+2S
2=S
1+S
3+2
(或=(
+
)
2).
点评:本题主要考查了全等三角形的性质以及三角形面积公式的灵活运用.要注意(4)中要分AB,CD平行和不平行两种情况来求解.

 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案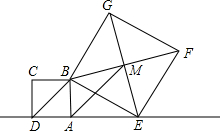 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.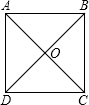 如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有
如图,正方形ABCD的对角AC,BD交于点O,则结论①AB=BC=CD=DA;②AO=BO=CO=DO;③AC⊥BD中正确的有
