练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
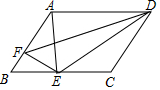
    7．如图，点E为?ABCD的边BC上一点，线段AE的垂直平分线恰好经过点D且交AB于点F，△BEF和△CDE的周长分别为8和13，则?ABCD的周长为21．

    分析 由线段垂直平分线的性质得出EF=AF，DE=AD，由三角形周长得出BE+EF+BF=BE+AF+BF=BE+AB=8，CE+CD+DE=CE+CD+AD=13，即可得出答案．

    解答 解：∵线段AE的垂直平分线恰好经过点D且交AB于点F，
    ∴EF=AF，DE=AD，
    ∵△BEF和△CDE的周长分别为8和13，
    ∴BE+EF+BF=BE+AF+BF=BE+AB=8，CE+CD+DE=CE+CD+AD=13，
    ∴?ABCD的周长为：AB+AD+CD+BC=（AB+BE）+（CE+CD+AD）=8+13=21；
    故答案为：21．

    点评 此题考查了平行四边形的性质以及线段垂直平分线的性质．此题难度不大，注意掌握数形结合思想与转化思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．要反映宁都县一天内气温的变化情况宜采用折线统计图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

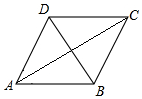    18．如图，菱形ABCD的边长为20，∠DAB=60，对角线为AC和BD，那么菱形的面积为（　　）
    A．50$\sqrt{3}$B．100$\sqrt{3}$C．200$\sqrt{3}$D．400$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．某市为了分析全市9600名初中毕业生的中考数学考试成绩，共抽取15本试卷进行调查，其中每本试卷都是30份，该调查的样本容量是450．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．五一节期间，电器市场火爆，某商店需要购进一批电视机和洗衣机，根据市场调查，电视机与洗衣机的进价和售价如下表：
    类别电视机洗衣机
    进价（元/台）18001500
    售价（元/台）20001600
    若该商店计划电视机和洗衣机共100台，设购进电视机x台，获得的总利润y元．
    （1）求出y与x的函数关系；
    （2）已知商店最多筹集资金161800元，求购进多少台电视机，才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多？并求出最多利润．（利润=售价-进价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，已知菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=2$\sqrt{2}$，BD=4，则菱形ABCD的面积为（　　）
    A．2$\sqrt{2}$B．4$\sqrt{2}$C．8$\sqrt{2}$D．16$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．为了解某小区居民的日用电情况，居住在小区的一名同学随机抽查了15户家庭的日用电量，具体结果如下表所示：
    日用电量/度567810
    户数2543l
    则关于这15户家庭的日用电量，下列说法正确的是（　　）
    A．众数是10度B．平均数是7度C．中位数是6度D．中位数是7度

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．第24届冬季奥林匹克运动会，将于2022年2月在北京市和张家口市联合举行．某校寒假期间组织部分滑雪爱好者参加冬令营集训．训练期间，冬令营的同学们都参加了“单板滑雪”这个项目40次的训练测试，每次测试成绩分别为5分，4分，3分，2分，1分五档．甲乙两位同学在这个项目的测试成绩统计结果如图所示．

    根据上图判断，甲同学测试成绩的众数是3；乙同学测试成绩的中位数是3；甲乙两位同学中单板滑雪成绩更稳定的是乙同学．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列命题：①三角形的一条中线将三角形分成面积相等的两部分；②平行于同一条直线的两条直线互相平行；③若|a|=|b|，则a=b；④对于任意x，代数式x2-6x+10的值总是正数．其中正确命题的个数是（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    同步练习册答案