练习册

  • 练习册
  • 试题
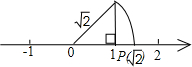
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图作一个等腰直角三角形，以数轴的原点为旋转中心，将过原点的斜边顺时针旋转，使斜边的另一端点落在数轴正半轴的点P处，则点P表示的数是
    		2
    ；这种研究和解决问题的方式，体现的数学思想方法是（　　）
    A、数形结合B、代入
    C、换元D、归纳
    分析：根据题意，分析题意中作图的方法，体会其中的思想，即可得答案．
    解答：解：根据题意，先根据勾股定理，得到长为
    		2
    的线段，
    再旋转可得P表示的数，从中体现了数形结合的思想，
    故选A．
    点评：本题考查学生对数学常见方法的把握，要求学生了解常见的数学思想、方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•锦州）如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．
    （1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；
    （2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；
    （3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=
    12
    ∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，将一块腰长为
    		5
    的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（-1，0），点B在抛物线y=ax2+ax-2上，
    （1）点A的坐标为
    （0，2）
    （0，2）
    ，点B的坐标为
    （-3，1）
    （-3，1）
    ；抛物线的解析式为
    y=
    1
    2
    x2+
    1
    2
    x-2
    y=
    1
    2
    x2+
    1
    2
    x-2
    ；
    （2）在抛物线上是否还存在点P（点B除外），使△ACP是以AC为直角边的直角三角形？若存在，请求出所有点P的坐标；若不存在，请说明理由．
    （3）若点D是（1）中所求抛物线在第三象限内的一个动点，连接BD、CD．当△BCD的面积最大时，求点D的坐标．
    （4）若点P是（1）中所求抛物线上一个动点，以线段AB、BP为邻边作平行四边形ABPQ．当点Q落在x轴上时，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2014年中考数学二轮精品复习归纳猜想型问题练习卷（解析版） 题型：解答题

    如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．


    （1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；
    （2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；
    （3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

     

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（辽宁锦州卷）数学（解析版） 题型：解答题

    如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．

    （1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；

    （2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；

    （3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=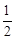∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2013年辽宁省锦州市中考数学试卷（解析版） 题型：解答题

    如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．
    （1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；
    （2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；
    （3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

    查看答案和解析>>

    同步练习册答案