
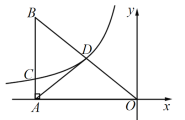
【题目】如图,函数![]() 的图象经过
的图象经过![]() 斜边
斜边![]() 的中点
的中点![]() ,与直角边
,与直角边![]() 相交于
相交于![]() ,连结
,连结![]() .若
.若![]() ,则
,则![]() 的周长为( )
的周长为( )
A.12B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过点D作DE⊥AO于点E,设点D(a,b),根据点D在函数![]() 的图象上可得DE·OE=1,根据∠BAO=90°,点D为OB的中点,可得AD=DO=3,根据勾股定理可得DE2+OE2=DO2=9,进而可得(DE+OE)2=11,由此可求得DE+OE=
的图象上可得DE·OE=1,根据∠BAO=90°,点D为OB的中点,可得AD=DO=3,根据勾股定理可得DE2+OE2=DO2=9,进而可得(DE+OE)2=11,由此可求得DE+OE=![]() ,进而求得
,进而求得![]() ,最后根据相似三角形的性质即可求得答案.
,最后根据相似三角形的性质即可求得答案.
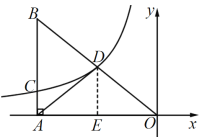
解:过点D作DE⊥AO于点E,
设点D(a,b),
则DE=b,OE=-a,
∵点D在函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴ab=-1,
∴DE·OE=-ab=1,
∵∠BAO=90°,点D为OB的中点,
∴AD=DO=3,
∴在Rt△DOE中,DE2+OE2=DO2=9,
∴(DE+OE)2= DE2+OE2+2 DE·OE
=9+2
=11
∴DE+OE=![]() (舍负)
(舍负)
∴![]() ,
,
∵点D为OB的中点,
∴DO=![]() ,
,
∵∠BAO=90°,DE⊥AO
∴∠BAO=∠DEO=90°,
∴DE∥AB,
∴△DEO∽△BAO,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
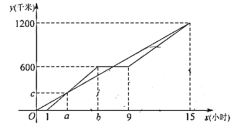
【题目】甲、乙两车沿同一条道路从![]() 地出发向1200
地出发向1200![]() 外的
外的![]() 地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达
地输送紧急物资,甲在途中休息了3小时,休息前后的速度不同,最后两车同时到达![]() 地,如图甲、乙两车到
地,如图甲、乙两车到![]() 地的距离
地的距离![]() (千米)与乙车行驶时间
(千米)与乙车行驶时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
(1)甲车休息前的行驶速度为 千米/时,乙车的速度为 千米/时;
(2)当9≤![]() ≤15,求甲车的行驶路程
≤15,求甲车的行驶路程![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)直接写出甲出发多长时间与乙在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数,
为常数,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.设该抛物线的顶点为
点.设该抛物线的顶点为![]() ,其对称轴与
,其对称轴与![]() 轴的交点为
轴的交点为![]() .
.
(1)求该抛物线的解析式;
(2)![]() 为线段
为线段![]() (含端点
(含端点![]() )上一点,
)上一点,![]() 为
为![]() 轴上一点,且
轴上一点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②当![]() 取最大值时,将线段
取最大值时,将线段![]() 向上平移
向上平移![]() 个单位长度,使得线段
个单位长度,使得线段![]() 与抛物线有两个交点,求
与抛物线有两个交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年中国“两会时间”
年中国“两会时间”![]() 月
月![]() 日正式开启,特殊时期召开的中国两会备受世界瞩目.某校为让学生进一步了解
日正式开启,特殊时期召开的中国两会备受世界瞩目.某校为让学生进一步了解![]() 年“两会”热点,计划开展关于两会的宣讲活动,开展活动之前,教务处随机抽取若干名学生,对“你最想听的宣讲内容”进行了调查,有
年“两会”热点,计划开展关于两会的宣讲活动,开展活动之前,教务处随机抽取若干名学生,对“你最想听的宣讲内容”进行了调查,有![]() .民生改善、
.民生改善、![]() .国家治理、
.国家治理、![]() .生态文明建设、
.生态文明建设、![]() .法治保障四项宣讲内容,经统计,被调查学生按学校要求,并结合自身的兴趣,每人从这四项宣讲内容中选择一项现将调查结果绘制成如下两幅不完整的统计图.
.法治保障四项宣讲内容,经统计,被调查学生按学校要求,并结合自身的兴趣,每人从这四项宣讲内容中选择一项现将调查结果绘制成如下两幅不完整的统计图.
结合图中信息解答下列问题:
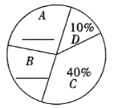
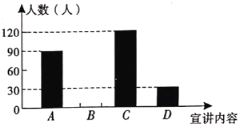
(1)请将两幅统计图补充完整,所抽取学生最想听的宣讲内容的众数是_____;
(2)在这次调查中,哪项宣讲内容的选择人数少于各项宣讲内容选择人数的平均数?
(3)若本校一共有![]() 名学生,请估计“最想听国家治理”的人数.
名学生,请估计“最想听国家治理”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() (如图).以线段
(如图).以线段![]() 为边向外作等边三角形
为边向外作等边三角形![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 并延长交线段
并延长交线段![]() 于点
于点![]() .
.
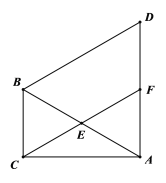
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)连接![]() ,交
,交![]() 于点
于点![]() .
.
①若![]() ,求
,求![]() 的长;
的长;
②作![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
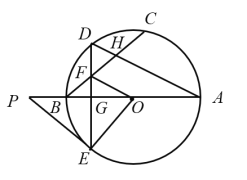
【题目】如图,在半径为![]() 的
的![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 中点,连接
中点,连接![]() ,交
,交![]() 于点
于点![]() ,弦
,弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)连接![]() ,求证:
,求证:![]() ;
;
(3)当点![]() 在
在![]() 上运动时,连接
上运动时,连接![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
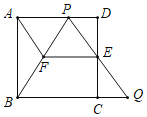
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备今年春季开工前美化厂区,计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
(2)若工厂每天需付给甲队的绿化费用为0.4万元,乙队为0.5万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com