
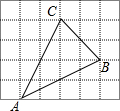
 网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,
网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,分析 (1)根据三角形的面积=正方形的面积-三个角上三角形的面积即可得出结论.
(2)作出AB边的高CE,根据面积相等求出CE,根据正弦是角的对边比斜边,可得答案.
解答  解:(1)S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×4
解:(1)S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×4
=16-4-2-4
=6.
故答案为6.
(2)CE⊥AB于E,
由勾股定理得AB=AC=2$\sqrt{5}$,
∵$\frac{1}{2}$AB•CE=6,
∴CE=$\frac{2×6}{2\sqrt{5}}$=$\frac{6}{5}$$\sqrt{5}$,
sinA=$\frac{CE}{AC}$=$\frac{\frac{6}{5}\sqrt{5}}{2\sqrt{5}}$=$\frac{3}{5}$.
点评 本题考查勾股定理、锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间的距离是两点间的线段 | |
| B. | 同一平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 与同一条直线垂直的两条直线也垂直 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3a)2=-9a2 | B. | $\frac{-a+b}{a+b}$=-1 | C. | 2a2-1=(2a+1)(2a-1) | D. | a3-4a3=-3a3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{{3}^{2}}$ | B. | -$\sqrt{(-3)^{2}}$ | C. | (-$\sqrt{\frac{1}{3}}$)2 | D. | $\sqrt{(-\frac{1}{3})^{-2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是( )
星期天,小宇同学骑自行车从家出发到图书馆查阅有关资料,之后就返回了家,如图反映了小宇离家的路程y(米)与骑车时间x(分)的函数关系.从图象得到下列信息,错误的是( )| A. | 小宇家与图书馆之间路程是3千米 | |
| B. | 小宇在图书馆查阅资料花去了42分钟 | |
| C. | 小宇从图书馆骑车回家用了10分钟 | |
| D. | 小宇从家到图书馆骑车速度比返回的速度慢 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
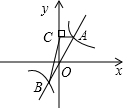 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.
华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com