
分析 先利用完全平方公式得到原式=$\frac{1}{2}$[(a-b)2+(b-c)2+(c-a)2],再分别计算(a-b)、(b-c)、(c-a),然后利用整体代入的方法计算.
解答 解:a2+b2+c2-ab-bc-ac=$\frac{1}{2}$[2a2+2b2+2c2-2ab-2bc-2ac]
=$\frac{1}{2}$[(a-b)2+(b-c)2+(c-a)2]
∵a=2004x+2000,b=2004x+2002,c=2004x+2004,
∴a-b=-2,b-c=-2,c-a=4,
∴原式=$\frac{1}{2}$[(-2)2+(-2)2+42]
=12.
点评 此题考查因式分解的运用,掌握完全平方公式是解决问题的关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
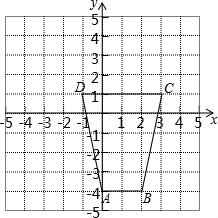 如图:
如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com