
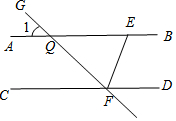
 如图,已知AB∥CD,GF分别交AB,CD于点Q,F,EF平分∠GFD,若∠1=40°,求∠BEF的度数.
如图,已知AB∥CD,GF分别交AB,CD于点Q,F,EF平分∠GFD,若∠1=40°,求∠BEF的度数. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
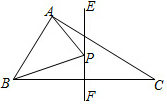 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是7.
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则△ABP周长的最小值是7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
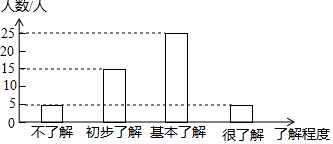 大同中学德育处针对同学们对厦门地铁建设情况的了解程度进行随机抽样调查,并制成如下统计图,请根据图中的信息,解答下列问题:
大同中学德育处针对同学们对厦门地铁建设情况的了解程度进行随机抽样调查,并制成如下统计图,请根据图中的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
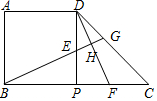 ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.
ABPD是一个边长为1的正方形,△DPC是一个直角边长为1的等腰直角三角形,把正方形ABPD和△DPC拼成一个如图所示的直角梯形,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF=x,BE的延长线分别交DF、DC于H、G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com