
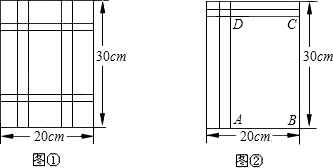
分析 因为每个竖彩条的宽为3x,图中有两个竖条,所以得到AB=20-2•3x=20-6x,又每个横彩条的宽为2x,图中有两个横条,所以BC=30-2•2x=30-4x,然后用AB•BC即为矩形ABCD的面积,从题中已知可知矩形ABCD的面积等于总体面积的$\frac{2}{3}$,根据题中的等量关系:矩形ABCD的面积=(1-$\frac{1}{3}$)×30×20,列出方程求解,再根据条件取值.
解答 解:可设每个横彩条的宽为2x,则每个竖彩条的宽为3x.
则AB=(20-6x)cm,AD=(30-4x)cm,矩形的面积=(20-6x)(30-4x)=24x2-260x+600;
故答案是:(20-6x),(30-4x),(24x2-260x+600);
根据题意,得24x2-260x+600=(1-$\frac{1}{3}$)×20×30,
整理,得6x2-65x+50=0,
解方程,得x1=$\frac{5}{6}$,x2=10(不合题意,舍去),
则2x=$\frac{5}{3}$,3x=$\frac{5}{2}$,
答:每个横、竖彩条的宽度分别为$\frac{5}{3}$cm,$\frac{5}{2}$cm.
点评 本题考查了一元二次方程的应用.用含x的代数式正确表示矩形ABCD的长与宽是列对方程的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
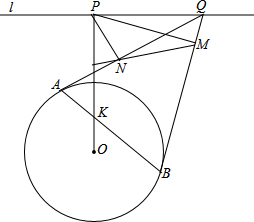 如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.
如图,圆O(圆心为O)与直线l相离,作OP⊥l,P为垂足.设点Q是l上任意一点(不与点P重合),过点Q作圆O的两条切线QA和QB,A和B为切点,AB与OP相交于点K.过点P作PM⊥QB,PN⊥QA,M和N为垂足.求证:直线MN平分线段KP.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0组 | B. | 1组 | C. | 2组 | D. | 3组 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com